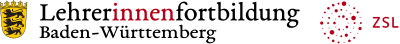Gemeinsame Aufträge der Teams
Gleicht eure Teilermengen, insbesondere T100 und T105, ab. Identifiziert, besprecht und beseitigt Fehler, falls nötig.
Stellt euch gegenseitig eure ausformulierten Vorgehensweisen von Aufgabe 2 und 3b der Teamarbeit vor. Vergleicht und diskutiert sie (besser/geschickter/einfacher/schneller/...).
a.) Stellt alle Teilermengen T2 bis T20 auf .
T2 = {1; 2}; T3 = {1; 3}; T4 = {1; 2; 4}; T5 = {1; 5}; T6 = {1; 2; 3; 6}; T7 = {1; 7};
T8 = {1; 2; 4; 8}; T9 = {1; 3; 9}; T10 = {1; 2; 5; 10}; T11 = {1; 11}; T12 = {1; 2; 3; 4; 6; 12}
T13 = {1; 13}; T14 = {1; 2; 7; 14}; T15 = {1; 3; 5; 15}; T16 = {1; 2; 4; 8; 16}; T17 = {1; 17}
T18 = {1; 2; 3; 6; 9; 18}; T19 = {1; 19}; T20 = {1; 2; 4; 5; 10; 20}
b.) Wovon hängt es ab, ob die Anzahl an Teilern einer Zahl gerade oder ungerade ist?
Quadratzahlen haben eine ungerade Anzahl an Teilern, Nicht-Quadratzahlen haben eine gerade Anzahl an Teilern.
a.) Stellt einige Zahlen auf, in deren Primfaktorzerlegung jede Primzahl höchstens einmal vorkommt. Welche davon enden mit der Ziffer 0?
Jede solche Zahl, in deren Primfaktorzerlegung sowohl die Primzahl 2, als auch die 5 enthalten ist, endet mit der Ziffer 0.
b.) Agentin Nü multipliziert alle Primzahlen zwischen 1 und 50. Agent Mü weiß sofort, wie viel mal die Ziffer 0 am Ende des Ergebnisses steht. Ihr auch? Erklärt eure Idee.
Es gibt genau eine gerade Primzahl: Die Zahl 2. Diese erzeugt in der angegebenen Multiplikation zusammen mit der Primzahl 5 den Faktor 10. Einen weiteren Faktor 10 gibt es innerhalb der Primzahlen nicht. Somit steht die Ziffer 0 genau einmal am Ende des Ergebnisses.
c.)* Agent Mü multipliziert alle natürlichen Zahlen zwischen 1 und 50 (und erhält also 50!). Agentin Nü überlegt einen Moment, dann weiß sie, wie viel mal die Ziffer 0 am Ende des Ergebnisses steht. Ihr auch? Erklärt eure Idee.
Es gibt genau acht Faktoren, in deren Primfaktorzerlegung die Zahl 5 einmal vorkommt (5, 10, 15, 20, 30, 35, 40, 45) und zwei Faktoren (25, 50) in deren Primfaktorzerlegung die 5 zweimal auftritt. Somit enthält die Primfaktorzerlegung des Produktes zwölf Mal den Faktor 5. Der Faktor 2 ist mehr als zwölf Mal vorhanden, es entstehen also zwölf „10er“, damit endet die Zahl 50! mit genau zwölf Nullen.
Die Abbildung zeigt ein sogenanntes Hasse-Diagramm für die Teilermenge der Zahl 72. Es stellt eine schöne Verknüpfungsmöglichkeit zwischen der Primfaktorzerlegung und der Teilermenge dar.
a.) Die Teilermenge ist direkt ablesbar. Die Primfaktorzerlegung ist auch sichtbar, man muss aber ein wenig „indirekt“ im Diagramm lesen. Wie? Stellt die Primfaktorzerlegung der Zahl 72 mithilfe des Hasse-Diagramms dar.
Die Breite des Rechtecks besteht aus drei Stäben. Diese gehören zum Primfaktor 2, da ein „nach rechts wandern“ der Multiplikation mit 2 entspricht. In der Primfaktorzerlegung ist die 2 als dreimal enthalten. Nach unten entspricht der Multiplikation mit 3, dazu sind zwei Verbindungen im Diagramm enthalten, die 3 kommt also zweimal vor. Somit lautet die Primfaktorzerlegung: 72 = 2 · 2 · 2 · 3 · 3
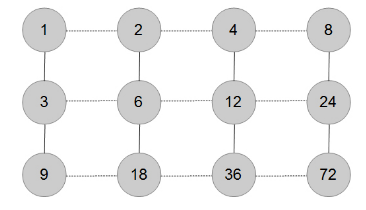
b.)Stellt weitere Hasse-Diagramme für die folgenden Zahlen auf:
→18 →32 →50 →24 →200 →*60 →**504
Vergrößern Abbildung weiterer Hasse-Diagramme
Anmerkung: Die Hasse-Diagramme kann man auch als Graphen interpretieren. Ein Hassediagramm ist sozusagen ein „Teilergraph“, der die Teilerstruktur einer Zahl veranschaulicht.
c.) Aus der Primfaktorzerlegung lässt sich schnell ableiten, wie viele Teiler die zugehörige natürliche Zahl hat. Wie, das lässt sich anhand der Hasse-Diagramme veranschaulichen. Ermittelt die zugehörige Methode und erklärt sie anschaulich mit Hasse-Diagrammen.
Die Hasse-Diagramme ergeben geometrisch betrachtet eine Linie, ein Rechteck oder einen Quader (bei bis zu drei unterschiedlichen Primfaktoren). Die Anzahl an Knoten (= Teiler) erhält man aus der Länge, dem „Flächeninhalt“ bzw. dem „Volumen“. Die Anzahl an Knoten entlang einer Kante ergeben sich aus den um 1 erhöhten Häufigkeiten der Primfaktoren in der Primfaktorzerlegung.
Beispiel: In der 60 ist der Primfaktor 2 mit Häufigkeit zwei, der Primfaktor 3 mit Häufigkeit eins und der Primfaktor 5 mit Häufigkeit 1 enthalten. Der Quader hat also eine Kante mit 3 (= 2+1) Knoten und zwei Kanten mit jeweiliger Länge 2 (= 1+1) Knoten. Somit befinden sich in der Teilermenge der Zahl 60 genau 3·2·2 = 12 Teiler.
-
* Der Geheimdienst hat in den letzten Jahren viel gearbeitet und so konnten einige verdächtige Personen eingesperrt werden. Nachdem aber Ihre Majestät, die große Zahl Pi, heute Geburtstag hat, sollen einige der Gefangenen zur Feier des Tages in die Freiheit entlassen werden. Dazu wird per Anordnung so vorgegangen: 100 verschlossene Zellen werden mit den Zahlen von 1 bis 100 durchnummeriert. Jetzt gehen nacheinander 100 Wärter an den Türen vorbei und drehen ihren Schlüssel so um, dass jede verschlossene Türe geöffnet und jede geöffnete Tür erneut geschlossen wird. Der erste Wärter dreht an jeder Tür seinen Schlüssel um (und öffnet somit alle Türen). Der zweite Wärter dreht seinen Schlüssel an jeder zweiten Tür, der dritte an jeder dritten Türe, usw. (sie fangen immer bei 1 mit dem Zählen an und gehen aufsteigend vor). Nachdem es nur 98 Gefangene gibt, verkündet die große Zahl Pi zur Überraschung aller Geburtstagsgäste noch folgenden Zusatz: „Meine beiden besten Agenten, Mü und Nü, dürfen sich eine der 100 Zellen frei auswählen, bevor die Gefangenen auf die restlichen Zellen verteilt werden. Wenn ihre Zellentür am Ende geöffnet ist, so bekommen sie ihre Zellentür mit 100 multipliziert in Dukaten ausbezahlt. Falls nicht … aber das kommt ja nicht vor, sie sind ja schließlich Superagenten!“.
Helft Agentin Nü und Agent Mü, welche beiden Zellen sollten sie wählen? Begründet eure Wahl.
Die Zellentüren sind am Ende geöffnet, wenn eine ungerade Anzahl an Wärtern den Schlüssel im Schloss gedreht haben. Diese Zellen entsprechen den Nummern mit ungeradzahlig vielen Teilern. Das sind die Quadratzahlen. Mü und Nü sollten also die höchstmöglichen Quadratzahlen wählen, also die 100 und die 81.
Teilermengen und Primfaktorzerlegungen – Lösungen: Herunterladen [odt][283 KB]
Teilermengen und Primfaktorzerlegungen – Lösungen: Herunterladen [pdf][265 KB]
Weiter zu kgV und ggT