Grundlagen

Vergrößern Quelle: ZPG IMP

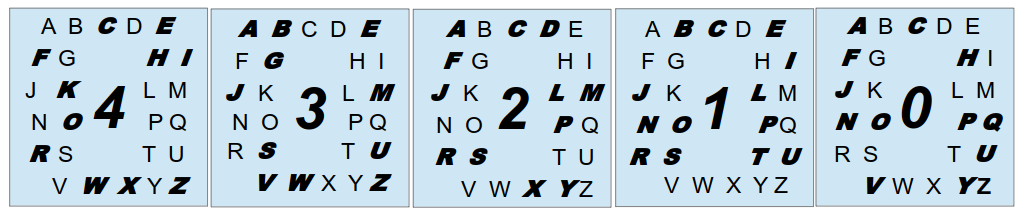
Agentin Nü und Agent Mü, zwei Geheimdienstler im Zeichen der Krone Ihrer Majestät, der großen Zahl Pi, stehen vor einem Rätsel. Sie haben den Teil einer verschlüsselten Nachricht erhalten, den du in der Abbildung siehst. Während Agent Mü noch nachdenkt, hat Agentin Nü schon eine Idee, denn auf dem Boden lagen auch noch die unten abgebildeten Karten voller Buchstaben und je einer Zahl.

„Das hat bestimmt etwas mit den Binärzahlen zu tun...!?“, denkt Agentin Nü laut nach.

„Aber was??“, rätselt Agent Mü und auch Nü hat keine Antwort darauf. Kannst du helfen?

Deine Aufträge:

1. Entschlüssele den Code.

   Wenn du einige Minuten nicht weiterkommst, wende dich an dein Hauptquartier (=Lehrerpult), dort gibt es durchnummerierte Hilfekärtchen. Nimm aber nur das jeweils nächste Kärtchen, nicht alle auf einmal. Beginne mit Hilfekärtchen 1.

   Entschlüsselter Code: __ __ __ __ __ __ __   __ __ __

2. a) Erkläre am Beispiel der Zahl 18, wie man zum zugehörigen Buchstaben kommt.

   b) Beschreibe, wie man die Zahl zum Buchstaben F bekommt, wenn man sie verschlüsseln möchte.

   c)* Lege eine vollständige Dechiffriertabelle für die Kärtchen an, d.h. eine Tabelle, die jedem Buchstaben seine Codezahl zuordnet.

3. Die Zahlen auf den Kärtchen sind nicht nur geschickt, falls die Kärtchen einmal durcheinander kommen. Sie haben auch eine mathematische Bedeutung für das Stellenwertsystem der Binärzahlen.

   Auch hierzu findest du wieder Hilfekärtchen, wenn du nicht weiterkommst.

   a) Erkläre diese Bedeutung.

   b) Im Alltag verwenden wir das dezimale Stellensystem. Hier gibt es die gleiche Struktur, das heißt auch hier treten diese Zahlen in ganz ähnlicher Bedeutung auf. Vergleiche das Dezimalsystem und das Binärsystem, gehe dabei insbesondere auf diese Bedeutung ein.

Binärzahlen-Grundlagen, Aufgabe 1., Hilfekärtchen 1:

Stelle die Zahlen im Binärsystem dar.

Binärzahlen-Grundlagen, Aufgabe 1., Hilfekärtchen 2:

Du weißt nicht mehr, wie die Binärdarstellung funktioniert? Vielleicht hilft dir ja schon ein einziges Beispiel: Die Zahl 13 schreibt man im Binärsystem beispielsweise so: 1101₂

Nebenbei bemerkt: Es ist wichtig, dass man die Zahlen im zugehörigen Stellenwertsystem liest. Leider gibt es keine einheitliche Schreibweise um kenntlich zu machen, dass man sich im Binärsystem befindet. Wir verwenden hier die Schreibweise mit der tiefgestellten 2 unten rechts. Es gibt aber auch andere Schreibweisen, z.B. eine Klammer mit einer tiefgestellten 2 oder auch nur ein kleines b am Ende der Zahl. Es ist also alles dasselbe, nur anders aufgeschrieben: 1101₂ = (1101)₂ = 1101b.

Binärzahlen-Grundlagen, Aufgabe 1., Hilfekärtchen 3:

Erinnerst du dich noch nicht? Kein Problem, hier nochmals die Erklärung zum „Strickmuster“ des Binärsystems. Es besteht nur aus den beiden Ziffern 0 und 1. Deshalb geben die einzelnen Stellen keine Einer, Zehner, Hunderter, …-Stellen an, sondern Einer, Zweier, Vierer, Achter, Sechzehner usw.

Die Stellen werden auch hier von rechts nach links größer. Die Zahl 10011₂ besteht somit – von rechts nach links – aus 1 Einer, 1 Zweier, 0 Vierer, 0 Achter und 1 Sechzehner, stellt also die Zahl 1+2+16=19 im Dezimalsystem dar.

Wandle nun alle Zahlen des Codes in das Binärsystem um. Wenn du weiterhin Schwierigkeiten dabei hast, wende dich an deinen Lehrer.

Binärzahlen-Grundlagen, Aufgabe 1., Hilfekärtchen 4:

Du hast die Zahl 12 erfolgreich als 1100₂ dargestellt?! Diese könnte, wenn man 5 Stellen berücksichtigen möchte (wegen der 5 Kärtchen), auch als 01100₂ geschrieben werden.

Betrachte nun die Buchstaben genauer: Manche sind normal gedruckt, manche fett. Was könnte das bedeuten?

Binärzahlen-Grundlagen, Aufgabe 1., Hilfekärtchen 5:

Für die Zahl 12 = 01100₂ : Suche nach dem Buchstaben, der auf den Kärtchen 4, 1 und 0 normal-, und auf den Kärtchen 3 und 2 fettgedruckt dargestellt ist. Dies ist nur der Buchstabe M. Fahre so mit den anderen Zahlen fort.

Binärzahlen-Grundlagen, Aufgabe 4., Hilfekärtchen 1:

Die Stellen „Einer, Zweier, Vierer, ...“ können mathematisch auch anders benannt werden. Dabei macht man sich zunutze, dass das Binärsystem immer genau zwei Ziffern zur Wahl hat.

Binärzahlen-Grundlagen, Aufgabe 4., Hilfekärtchen 2:

Du hast Hilfekärtchen 1 gelesen, aber immer noch keine Idee? Dann hier noch ein kleiner Tipp: Stelle zunächst die mathematische Verbindung, zwischen der Zahl 2 und den Stellennamen Zweier, Vierer, Achter, … her. Wie kann man Zwei, Vier, Acht, … mit der Zahl 2 ausdrücken? Du hast es? Was ist dann mit den „Einern“?

Binärzahlen-Grundlagen, Aufgabe 4., Hilfekärtchen 3:

Verwende die Zahl 2 als Basis einer Potenz. Suche nacheinander jeweils einen Exponenten x so, dass 2^x als Ergebnis Sechzehn, Acht, Vier, Zwei und Eins ergibt. Vergleiche deine Ergebnisse mit den Zahlen auf den Kärtchen.

Binärzahlen: Herunterladen [odt][1 MB]

Binärzahlen: Herunterladen [pdf][402 kB]

Weiter zu Übungen