Das Fermat‘sche Prinzip
3. bis 6. Stunde
Als Einstieg wird zusammenfassend festgehalten:
Optische Phänomene können mit der geradlinigen Lichtausbreitung, der Reflexion und der Brechung beschrieben werden.
Es folgt eine Diskussion über die Gesetze der Lichtausbreitung.
Die Schülerinnen und Schüler kennen das Reflexionsgesetz. Für die Brechung können sie kein Gesetz angeben.
Fermat hat um 1650 ein Prinzip gefunden, dass das Verhalten des Lichts einleuchtend darstellt.
Das Fermat‘sche Prinzip
Von allen möglichen Wegen, die das Licht nehmen könnte, um von einem Punkt zu einem anderen Punkt zu gelangen, nimmt es den Weg, der die kürzeste Zeit erfordert.
Das Fluchten über einen krummen Besenstiel dient als Einstieg zur geradlinigen Lichtausbreitung. Für die Schülerinnen und Schüler ist es pausibel, dass dies der schnellste Weg ist.
Fermat und die geradlinige Lichtausbreitung
Licht breitet sich von Punkt zu Punkt geradlinig aus. Dies ist der kürzeste Weg, der auch die kürzeste Zeit erfordert.
Mit einem Perspektivwechsel kann das Fermat‘sche Prinzip für die Schülerinnen und Schüler anschaulicher unterrichtet werden. Wir untersuchen zuerst Laufwege an Land und im Wasser.
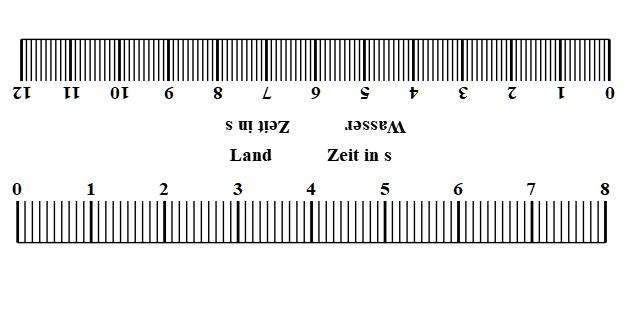
Abb. 11: Zeitlineal, v. Harten erstellt mit Veusz 2.2.1 u. gimp 2.8.22
Ein einfacher Zugang gelingt mit einem Zeitlineal. Die benötigte Zeit kann direkt abgelesen werden.
Zusatz:Die Schülerinnen und Schüler erstellen ein Zeitlineal. Je nachdem, welche Kompetenzen man stärken möchte, kann dies mit Bleistift oder mit einem Computer realisiert werden.
Als nächstes wird die Reflexion mit einem Arbeitsblatt untersucht. Für vorgegebene Strecken wird der Weg mit der kürzesten Zeit ermittelt.
00_oub_kopiervorlage_zeitlineal
01_oub_ab_fermat_reflexion_zeitlineal
Einfallswinkel und Reflexionswinkel werden bestimmt und verglichen.
02_oub_ab_fermat_reflexion_winkel
Die vorgegebenen Strecken sind eine didaktische Reduktion. Alle möglichen Wege müssen untersucht werden. Als Vertiefung oder Differenzierung bietet sich hier ein geometrischer Nachweis an.
03_oub_ab_fermat_reflexion_geometrie
Fermat und die Lichtreflexion
Bei der Reflexion gilt das Reflexionsgesetz. Der Lichtweg ist der kürzeste Weg und auch der Weg mit der kürzesten Zeit.
Heron von Alexandria (Heron-Verfahren) soll schon vor 2000 Jahren gezeigt haben, dass das Licht bei der Reflexion den kürzesten Weg nimmt.
Warum formulierte Fermat sein Prinzip mit dem Weg mit der kürzesten Zeit?
Bei der Brechung wird der schnellste Weg am Beispiel Land/Wasser mit einem Zeitlineal ermittelt. Das Geschwindigkeitsverhältnis an Land und im Wasser entspricht dem Verhältnis der Lichtgeschwindigkeiten in Luft und Glas (n = 1,5).
04_oub_ab_fermat_brechung_zeitlineal
Den Schülerinnen und Schülern wird mitgeteilt, dass das Geschwindigkeitsverhältnis dem von Luft und Glas entspricht. Sie sollen den Einfallswinkel und den Brechungswinkel bestimmen und mit dem entsprechenden Brechungsdiagramm vergleichen.
05_oub_ab_fermat_brechung_winkel
06_oub_kopiervorlage_brechungsdiagramm
Fermat und die Lichtbrechung
Bei der Brechung ist der Lichtweg nicht der kürzeste Weg. Es ist der Weg mit der kürzesten Zeit.
Auch hier sind die vorgegebenen Strecken eine didaktische Reduktion. Alle möglichen Wege müssen untersucht werden. Eine exakte Herleitung (Extremwertaufgabe) ist in dieser Klassenstufe nicht möglich. Für weitere Wegberechnungen kann ein Computer eingesetzt werden.
Tabellenkalkulation
Fermat_Brechung.ods
Scratch-Programm
Fermat_Brechung.sb2
Durch Verschieben der grünen Fahne in der Mitte der Bühne kann der Einfallswinkel verändert werden (Pfeiltasten). Der Zeitmesser i zeigt die benötigte Zeit an. Mit der Leertaste beginnt die Zeitmessung. Auf diese Weise kann der kürzeste Weg bestimmt werden.
Zusatz:Als Vertiefung können die Schülerinnen und Schüler den Algorithmus aufstellen und programmieren.
Anwendungen des Fermat‘schen Prinzip
5. Stunde
Die Umkehrbarkeit des Lichtweges ist eine einfache Folgerung aus dem Prinzip.
Aus dem Prinzip von Fermat folgt die Umkehrbarkeit des Lichtweges.
Zwei weitere Anwendungen können mit einem Arbeitsblatt erarbeitet werden.
1.
Der Lichtweg durch einen Glaskörper mit planparallelen Flächen soll mit dem Prinzip qualitativ ermittelt werden.
2.
Warme Luft hat eine geringere Dichte als kältere Luft. Entsprechend größer ist die Lichtgeschwindigkeit in der wärmeren Luft. Die Schülerinnen und Schüler können mit dieser Information auch eine Luftspiegelung erläutern.
Den Schülerinnen und Schülern werden die Aufgaben auf dem Arbeitsblatt mit der neuen Denkweise nicht leichtfallen. Ein Lehrer-Schüler-Gespräch ist eine sinnvolle Alternative.
07_oub_ab_fermat_anwendungen
Zusatz:
Aufgrund der abnehmenden Luftdichte wird die Lichtgeschwindigkeit in der Atmosphäre mit steigender Höhe immer größer. Damit lassen sich Sonnenuntergangsphänomene (z.B. vermeintlicher Sonnenstand) erklären.
An Hand eines elliptischen Spiegels mit seinen zwei Brennpunkten kann die Ellipse eingeführt werden, die eine zentrale Rolle bei den Planetenbewegungen spielt.
Die Schülerinnen und Schüler sollen nach dem Bildungsplan die Form einer Sammellinse mithilfe des Fermat'schen Prinzips qualitativ erklären können.
08_oub_ab_fermat_sammellinse
Hier kann man auch das Scratchprogramm fermat_sammellinse einsetzen.
fermat_sammellinse.sb2
Hier verändern die Schülerinnen und Schüler die Breite der Linsenblöcke derart, dass die Teilstrahlen sich im vorgesehenen Punkt treffen.
Ausblick
Am Ende dieser Einheit regt man eine Diskussion über das neue Konzept an.
Als Impuls kann man die These, dass alle Phänomene auch ohne Fermat erklärt werden könnten, einwerfen.
Im Gegensatz zur geometrischen Optik kann man Voraussagen über die Lichtgeschwindigkeit in verschiedenen optischen Medien machen.
Schülerfragen, woher das Licht weiß, welcher Weg der schnellste Weg ist, können hier nicht beantwortet werden. Eine Antwort dazu gibt die Quantenphysik. Die Physik bleibt für die Schülerinnen und Schüler spannend.
Andere Verfahren
Streckenmessung statt Zeitlineal
Die Schülerinnen und Schüler sind in der Lage über die Formel die Laufzeiten zu berechnen.
Scratch
Bei Scratch kann ein Objekt in eine bestimmte Richtung in x-er Schritten gehen. Die Schrittlänge ist unabhängig von der Richtung.
Am Strand kann z.B. mit 3-er Schritten und im Wasser mit 2-er Schritten gelaufen werden . D.h. die Geschwindigkeiten stehen im Verhältnis 3:2. Die Anzahl der Schritte ist damit proportional zur Zeit.
Die Schülerinnen und Schüler sollten nach dem Informatikunterricht in Klasse 7 in der Lage sein ein entsprechendes Programm zu erstellen.
Siehe Fermat_Brechung.sb2.
Tabellenkalkulation
Im Mathematikunterricht sollen die Schülerinnen und Schüler bei der Zinsrechnung eine Tabellenkalkulation verwenden. D.h. die Schülerinnen und Schüler können mit einer Tabellenkalkulation arbeiten. Sie können radizieren. Eine Rücksprache mit den Mathematiklehrerinnen und -lehrern ist zu empfehlen. Für die Streckenberechnung muss man den Satz des Pythagoras vorgeben.
Siehe Fermat_Brechung.ods.
Dynamische-Geometrie-Software
Hier bietet sich z.B. der Einsatz von Geogebra an. Für die Streckenlänge gibt es die Funktion Abstand[Punkt_1,Punkt_2].
Siehe Fermat_Brechung_Simulation.ggb.
Unterrichtsverlauf: Herunterladen [odt][4,4 MB]
Unterrichtsverlauf: Herunterladen [pdf][598 KB]
Weiter zu Die Sammellinse
