Multigraphen – andere Reihenfolge – Lösung

1. Königsberger Brückenproblem

   Man zeichnet einen Graphen direkt im „Stadtplan“ oder gleich als idealisierten Graphen:

   

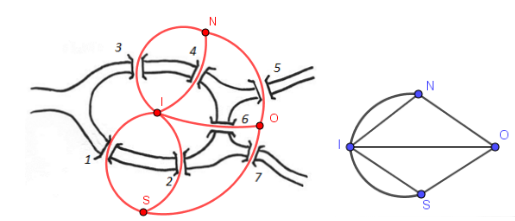
   siehe auch Graph in Aufgabe 3b) auf dem Arbeitsblatt

   Alle vier Knoten besitzen ungerade Ordnung. Da der Graph mehr als zwei ungerade Knoten besitzt, ist ein Rundgang unmöglich.

2. Das Nachtwächter-Problem

   

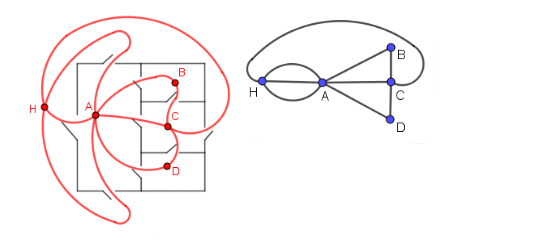
   Als Graph im Grundriss der Fabrikhallen und als idealisierter Graph (ist auch in Aufgabe 3d) abgebildet)

   Der Hof und jede der Hallen werden als Knoten und die Verbindungswege durch die Türen als Kanten aufgefasst.

   In allen Knoten trifft eine gerade Anzahl an Kanten zusammen. Da nur gerade Knoten auftreten, existiert ein geschlossener Eulerscher Kantenzug, der Rundgang ist möglich.

3. 

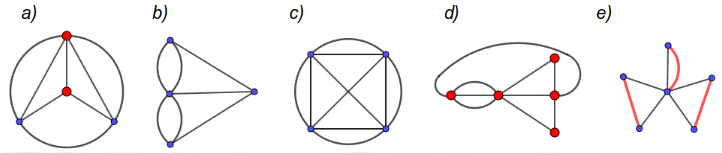
   Die Graphen a) bis d) sind Multigraphen, e) ist ein einfacher Graph ohne Mehrfachkanten.

   Bei a) ist ein offener EKZ möglich, beide ungeraden Start- bzw. Endknoten sind markiert.

   Bei b) und c) sind keine EKZ möglich, beide Graphen besitzen nur ungerade Knoten.

   Bei d) sind geschlossene EKZ möglich, da nur gerade Knoten auftreten (vgl. Aufg. 2).

   Bei e) sind mindestens 3 weitere Kanten nötig, damit alle Knoten gerade Ordnung haben.

4. Es müssen mindestens 2 Brücken ergänzt oder entfernt werden, individuelle Lösungen.

5. 

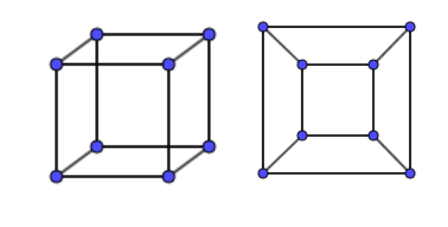
   Nein. In jeder Würfelecke stoßen 3 Kanten zusammen, der zugehörige Graph hat 8 ungerade Knoten und lässt sich daher nicht „in einem Zug“ zeichnen. Ein Graph heißt übrigens „planar“ oder „plättbar“, wenn er wie rechts zu sehen in der Ebene ohne Überschneidungen gezeichnet werden kann.

Multigraphen – andere Reihenfolge – Lösung: Herunterladen [odt][280 KB]

Multigraphen – andere Reihenfolge – Lösung: Herunterladen [pdf][215 KB]

Weiter zu Hamiltonkreise