Graphen als Tabellen – Übungen – Lösung
-
Nachbarschaftstabellen
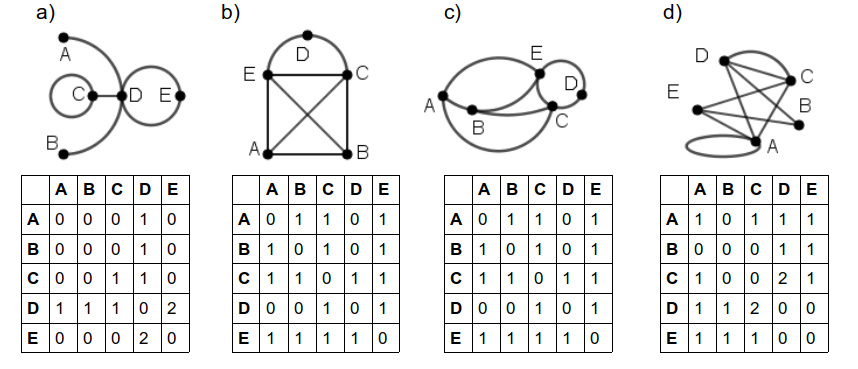
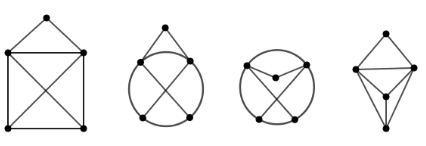
e) Die beiden Graphen b) und c) besitzen identische Nachbarschaftstabellen und sind daher isomorph. Rechts sind Graphen zu sehen, die ebenfalls wie b) und c) zum „Haus des Nikolaus“ isomporph sind.
-
Graph zur Tabelle
individuelle Lösungen, zwei Beispiele:
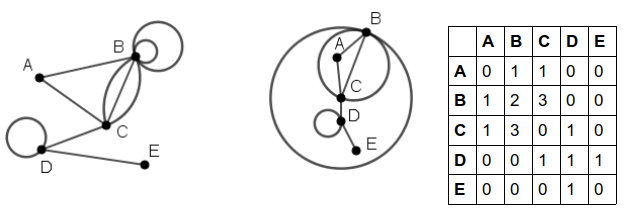
-
Nicht isomorphe Graphen
-
Beide Graphen enthalten zwei topologische „Dreiecke“ mit einer gemeinsamen Kante. Die beiden Knoten der Ordnung 3 liegen sich gegenüber.
-
Man kann z.B. die Kante zwischen den beiden Knoten mit Ordnung 3 als Achse betrachten und einen der „Flügel“ um diese Achse um 180° drehen.
-
Da jeder Knoten mit jedem anderen durch genau eine Kante verbunden ist, beschreiben beide Graphen einen vollständigen Graphen mit vier Knoten, sie sind also isomorph.
-
-
Isomorphe Graphen erkennen
-
Der mittlere Graph ist nicht zusammenhängend, er besteht aus 2 Teilgraphen, einem Drei- und Viereck. Der 1. und 3. Graph sind isomorph, sie bilden beide einen geschlossenen Ring.
-
Der rechte Graph hat 13 Knoten und einen Knoten der Ordnung 5 (Maximalgrad), was beide anderen Graphen nicht aufweisen. Dreht man einen der beiden ersten Graphen um 180° um einen seiner Mittelknoten, so erkennt man die topologische Äquivalenz schnell.
-
-
Isomorphie begründen
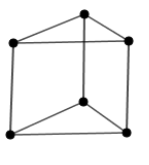
In jedem der Graphen gibt es zwei „Dreiecke“, bei denen jede Ecke des einen mit genau einer Ecke des anderen Dreiecks durch eine Kante verbunden ist, wie beim Prisma. Sie sind hamiltonsch, aber nicht eulersch. Wegen der Isomorphie genügt es dabei, einen der Graphen zu untersuchen.
Graphen als Tabellen – Übungen – Lösung: Herunterladen [odt][199 KB]
Graphen als Tabellen – Übungen – Lösung: Herunterladen [pdf][158 KB]
Weiter zu Logik
