Entdecken und Beweisen – Satz des Thales
-
Abwärts...
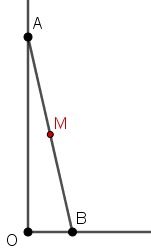
Eine 4m lange Leiter ist wie im Bild an eine senkrechte Wand gelehnt.
Wie bewegt sich ihr Mittelpunkt, wenn sie anfängt zu rutschen?
Simuliert die Situation mit GeoGebra. Gebt dazu die Befehle der 3. Spalte Schritt für Schritt in die Eingabezeile ein. Am Ende könnt ihr den Punkt A bewegen und den Punkt M beobachten. Bei Bedarf kann man im Kontextmenu (rechter Mausklick auf M) die „Spur von M“ anschalten.
Formuliert eure Vermutung schriftlich und versucht sie dann zu beweisen.
Dokumentiert die Argumentationsschritte übersichtlich im Heft.
Name
Eingabe / Defintion
Symbol
Beschreibung
1
Punkt O
O=(0,0)

Ursprung als O bezeichnen (lat. „Origo“)
2
Punkt P
P=(0,4)

P als Endpunkt auf y-Achse wählen
3
Punkt Q
Q=(4,0)

Q als Endpunkt auf y-Achse wählen
4
Strecke f
f=Strecke(O, P)

Strecke OP wird mit f bezeichnet
5
Punkt A
A=Punkt(f)

Punkt A auf Strecke f definieren
6
Strecke g
g=Strecke(O, Q)

Strecke O, Q
7
Kreis k
k=Kreis(A, 4)
Kreis mit Mittelpunkt A und Radius 4
8
Punkt B
B=Schneide(k, g)

Schnittpunkt von k, g
9
Strecke h
h=Strecke(A, B)

Strecke A, B
10
Punkt M
Mittelpunkt(A, B)

Mittelpunkt von A, B
11
Blende Punkt O und Kreis c aus, z.B. durch Anklicken im Algebrafenster.
-
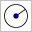
Zwei Kreise
Gegeben sind zwei Kreise mit den Durchmessern BC bzw. BD, die sich in den Punkten A und B schneiden. Zeige, dass C, A und D auf einer Geraden liegen.
-
Dreiecke vereinigt euch ...
Gegeben ist eine Strecke AB. Bestimme die Vereinigungsmenge aller Dreiecke ABC,
die bei C einen stumpfen Winkel haben.
-
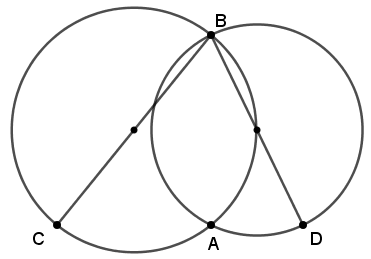
Gemeinsame Tangente
Gegeben sind zwei Kreise, die sich von außen im Punkt A berühren. Die Berührpunkte B und C haben eine gemeinsame Tangente und CD ist ein Kreisdurchmesser.
Zeige, dass Punkt A auf der Strecke DB liegt.
Entdecken und Beweisen – Satz des Thales: Herunterladen [odt][183 KB]
Entdecken und Beweisen – Satz des Thales: Herunterladen [pdf][83 KB]
Weiter zu Satz von Viviani
