Teilbarkeit und Teilbarkeitsregeln: Wiederholung
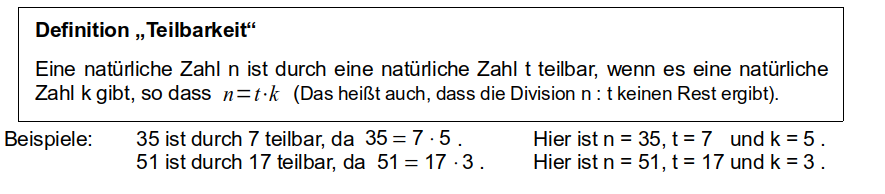
Die Frage nach der Teilbarkeit von natürlichen Zahlen spielt in der Zahlentheorie eine wichtige Rolle. Du kennst sicherlich schon einige Fakten und Regeln dazu oder hast zumindest schon einmal davon gehört. Diese wollen wir hier zuerst wiederholen und dann erweitern. Beginnen wir der Reihe nach. Zuerst muss man wissen, was man unter Teilbarkeit überhaupt versteht:
Aufträge:
THINK-PAIR-SHARE:
a.) Um die Teilbarkeit einer beliebigen natürlichen Zahl durch die Zahlen 2, 3, 5, 6, 9 und 10 zu untersuchen, hast du bereits Regeln kennen gelernt. Versuche dich zunächst in Stillarbeit an diese Regeln zu erinnern und schreibe alle, die du noch kennst, auf das dafür beigefügte Arbeitsblatt. Nach 5 Minuten darfst du dich leise mit deinem Nachbarn austauschen und ihr könnt eure Regeln gegenseitig korrigieren und ergänzen.
b.) Man unterscheidet „Endstellenregeln“ und „Quersummenregeln“ . Ordne die Regeln aus a.) wenn möglich einer der beiden Kategorien zu und begründe deine Zuordnung.
-
a.) Untersuche mithilfe der Regeln die folgenden Zahlen auf Teilbarkeit durch die Zahlen
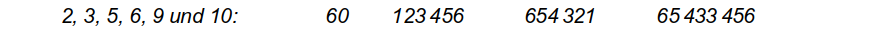
b.) a und b sind frei wählbare Ziffern (von 0 bis 9). Gib jeweils mindestens eine Möglichkeit für die Ziffern a und b so an, dass die Zahl 125 a3b
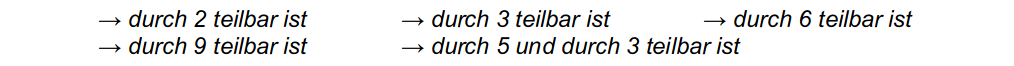
-
Die Zahlen a, b und t seien natürliche Zahlen. Formuliere zunächst ein paar konkrete Zahlenbeispiele für die folgenden Sätze zur Teilbarkeit. Begründe die Sätze dann mithilfe der (oben stehenden) Definition.
Es liegen Hilfekärtchen bereit, wenn du nicht weiterkommst.

-
a.) Überprüfe ohne Taschenrechner, ob die folgenden Summen jeweils durch 3 teilbar sind. Benenne und erkläre: In welchen Fällen nützt dir Satz 1 aus 3a.) etwas, wann nicht?
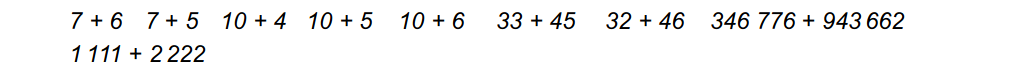
b.) Überprüfe, ob die folgenden Produkte jeweils durch 9 teilbar sind. Benenne und erkläre: In welchen Fällen nützt dir Satz 2 aus 3a.) etwas, wann nicht?
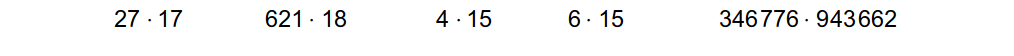
AB zu Aufgabe 1

AB zu Aufgabe 1, Seite 2 von 8
Aufgabe 3a, Hilfekärtchen 1:
Betrachte die folgenden Beispiele.
Begründe ohne die Summe zu berechnen, weshalb sie durch 7 teilbar ist:
28 + 35
14 + 77
Aufgabe 3a, Hilfekärtchen 2:
Betrachte weiterhin die Beispiele von Kärtchen 1. Begründe mithilfe der Definition, weshalb die einzelnen Summanden, also 28, 35, 14 und 77 durch 7 teilbar sind. Forme sie dazu so um, wie es in der Definition verlangt ist, also z.B. 28 = 7·4, füge dann diese Umformungen in die Summen ein.
Aufgabe 3a, Hilfekärtchen 3:
Mithilfe der einzelnen Zerlegungen von Hilfekärtchen 2 solltest du nun folgendes bereits notiert haben:
28 + 35 = 7·4 + 7·5
14 + 77 = 7·2 + 7·11
Klammere auf der rechten Seite jeweils die 7 aus und führe die Begründung vollends durch.
Aufgabe 3b, Hilfekärtchen 1:
Betrachte die folgenden Beispiele. Begründe ohne das Produkt zu berechnen, weshalb es durch 7 teilbar ist:
14·11
2111553·21
Aufgabe 3b, Hilfekärtchen 2:
Betrachte weiterhin die Beispiele von Kärtchen 1.Begründe mithilfe der Definition, weshalb einer der beiden Faktoren durch 7 teilbar ist. Füge dann die zugehörige Umformung in das Produkt ein.
Aufgabe 3b, Hilfekärtchen 3:
Mithilfe der Umformungen von Hilfekärtchen 2 solltest du nun folgendes bereits notiert haben:
14·11=7·2·11
2111553·21=2111553·7·3
Klammere in der Summe die 7 aus und führe die Begründung vollends durch.
Teilbarkeit und Teilbarkeitsregeln: Herunterladen [odt][390 KB]
Teilbarkeit und Teilbarkeitsregeln: Herunterladen [pdf][160 KB]
Weiter zu Weitere Regeln
