Aussagenlogik
5. Stunde: Sitzen, Rudern und Umfüllen – Logikrätsel und Graphen
| Ablauf und Inhalte | Hinweise |
|
Fokus: Graphen als heuristisches Hilfsmittel
|
|
Erläuterungen
In dieser Stunde sollen die SuS erkennen, dass Graphen als heuristisches Hilfsmittel zum Problemlösen sehr hilfreich sein können. Das symmetrische Sitzordnungsproblem in Aufgabe 1 stllet den Bezug zu den vorangegangenen Stunden her, insbesondere zu Hamilton-Kreisen. Während in dabei die Deutung der Stühle als Knoten noch naheliegend ist, werden ab Aufgabe 2 neue Blickwinkel eröffnet, bei denen Zustände als Knoten und deren Änderungen als gerichtete Kanten aufgefasst werden. In Aufgabe 2 sind dies z.B. Konstellationen am Ufer, in Aufgabe 3 Wassermengen in den Gefäßen. Gezeigt wird dies an einfachen „Klassikern“, die mit der Strategie des Vorwärtsarbeitens lösbar sind. Aus Sicht der Graphentheorie werden geeignete Kantenzüge einfacher Digraphen1 verwendet, um Logikrätsel übersichtlich zu lösen. Es wurde darauf verzichtet, Digraphen per Definition einzuführen, sie sollen nur intuitiv verwendet werden.
Mögliches Rätsel für den Einstieg in den Themenbereich Aussagenlogik zu Stundenbeginn:
Fehlerhafte Sätze2
(1) Dieser Sats enthält zwei Feler.
(2) Diser Satz endhält drei Fehler.
Jeder dieser beiden Sätze stellt im Sinne der Logik eine Aussage dar, die entweder wahr (richtig) oder falsch sein kann.
a) Welcher der beiden Sätze ist falsch, welcher richtig? Begründe deine Meinung.
b) Ändere in jeder Aussage ein Wort, so dass aus einer wahren Aussage eine falsche wird oder umgekehrt aus einer falschen Aussage eine richtige .
- a) Beide Sätze sind wahre Aussagen. Satz (1) enthält zwei orthographische Fehler (Sats, Feler). Satz (2) enthält drei Fehler, zwei orthographische (Diser, endhält) und einen mathematischen, nämlich den Zählfehler „drei“ statt „zwei“.
- b) Die Aussage von Satz (1) wird z.B. falsch , wenn man noch einen Rechtschreibfehler macht oder das Wort „vier“ statt „zwei“ verwendet, also einen mathematischen Fehler einbindet. Die Aussage von Satz (2) wird falsch, wenn er z.B. nur einen Rechtschreibfehler enthält oder man einen mathematischen Fehler einbaut, z.B. Durch Verwendung des Wortes „vier“ statt „drei“.
Man kann hier die im Vordergrund stehenden orthographischen Fehler von mathematischen Fehlern abgrenzen und ggf. auch weiterführende Aspekte der Aussagenlogik in den Blick nehmen, z.B. über die Negation der Ausssagen. Natürlich eigenen sich auch zahlreiche andere Rätsel zur Sensibilisierung für den Bereich der Aussagenlogik.3
Hinweise zu den einzelnen Aufgaben:
-
Geburtstagsrunde (Sitzordnung)
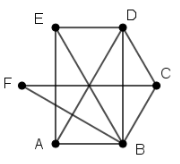
Im Unterricht werden die SuS wahrscheinlich mit einer gefundenen Lösung zufrieden sein. Die Klasse findet vielleicht beide Lösungen, aber es bleibt die Unsicherheit, ob damit wirklich alle Lösungen erfasst wurden. Erst durch die Frage nach der Existenz weiterer Lösungen kann der Nutzen der Veranschaulichung als Graph vermittelt werden. Damit dies durch kombinatorische Überlegungen auch gut geklärt werden kann, wurden die Bedingungen so gewählt, dass im Einführungsbeispiel nur zwei Sitzordnungen (Hamilton-Kreise) möglich sind: BFCDEAB , BFCDAEB. Es bietet sich an, von den Knoten der Ordnung 2 auszugehen, da diese zwischen ihren Nachbarknoten liegen müssen. Im Beispiel ist dadurch die Sequenz BFC (bzw. CFB) festgelegt. Die beiden Möglichkeiten lassen sich leicht folgern. Die Visualisierung kann mit einem Baumdiagramm an der Tafel erfolgen (oder alternativ mit der dafür konzipierten Datei 05_aug_ab_logik_graphen_Nr1loesung.ggb).
Das Rätsel lässt sich vielfältig modifizieren. In einer leichteren Variante könnte man z.B. auch zulassen, dass Anton neben Frieda sitzt, die beiden „Komplementärgraphen“ hierzu sind hier abgebildet. Dann gäbe es 7 Lösungen bzw. Hamiltonkreise: ABEDCFA, ABFCDEA, ADEBCFA, ADCFBEA, AEBDCFA, AEDCBFA und AEDBCFA.
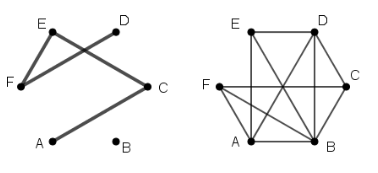
Eine Lösung wäre zwar schnell gefunden, aber die kombinatorische Frage nach allen möglichen Hamilton-Kreisen würde einige Zeit erfordern. Diese Variante eignet sich daher eher als differenzierende Zusatzaufgabe.
Es stehen weitere anspruchsvollere Varianten mit 3 oder 5 möglichen Sitzordnungen bereit (z.B. 05_aug_ab_..._Nr1_mit3kreisen_loesung.ggb). Der Rätseltext muss dann nur entsprechend angepasst werden, indem mehr oder weniger einschränkende Bedingungen formuliert werden. Beim Erstellen ähnlicher Rätsel bietet es sich prinzipiell an, rückwärts zu arbeiten, d.h. vom vollständigen Graphen auszugehen, sukzessive Bedingungen zu formulieren und die zugehörigen Kanten zu streichen.
-
Schwierige Überfahrt
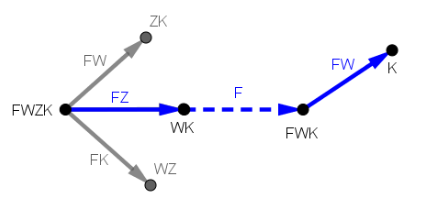
Die SuS werden dieses Problem sicher ohne Graphen, sondern mit Tabellen oder anderen informativen geeigneten Figuren lösen. Dann kann man in der Rückschau das übersichtliche Vorgehen mithilfe des relevanten Ausschnitts eines gerichteten Graphen als Lehrervortrag einführen. Dazu steht die GeoGebradatei 05_aug_ab_logik_graphen_Nr2_loesung.ggb zur Verfügung, mit der sich die Fahrten wie oben angedeutet nacheinander einblenden lassen, während die Argumentation vorgetragen wird. Eine größere Herausforderung für die Vertiefung bieten danach die ergänzenden Aufgaben Nr.3 und 6 auf dem Übungsblatt, bei denen es keinen Fährmann gibt, sondern alle Beteiligten gleichberechtigt rudern dürfen.
-
Hinweise zu Umfüllrätseln (Nr. 3 und 5) – graphisches Lösungsverfahren
Auf dem AB wurden zum Einstieg zwei einfachere Umfüllprobleme eingebunden. Die Lösungen lassen sich auch graphisch ermitteln. Das Verfahren wurde bei der Beschreibung des Hintergrunds am Beispiel der Aufgabe 3 ausführlich erläutert4. Für die Einbindung im Unterricht kann die Datei 05_aug_ab_umfuellgraphen_8-5-3.ggb eingesetzt werden, um den Gedankengang schrittweise und anschaulich zu entwickeln.
Ergänzend soll das Verfahren hier nochmals am Beispiel der komplexeren Aufgabe 5b) des Übungsblattes skizziert werden:
Es sollen 12 Liter Apfelsaft halbiert werden, die sich in einem großen Krug befinden. Zwei weitere leere Krüge mit 7 l bzw. 5 l Fassungsvermögen sind vorhanden … .
Man wählt sich ein passendes Parallelogramm (hier z.B. a = 7 LE, b = 5 LE, b = 5 LE, α = 60°), auf dessen Kanten man „Billiard spielt“. Mathematisch gesehen sucht man im zugrunde liegenden Graphen der Füllzustände den kürzesten Kantenzug vom Knoten (12,0,0) zum Knoten (6,6,0). Dabei beginnt man unten links im Knoten „0“, der dem Zustand (12,0,0) entspricht und visualisiert die Umschüttvorgänge durch Pfeile. Der Weg einer fiktiven Billiardkugel wird an den Kanten des Parallelogramms nach dem bekannten Reflexionsgesetz fortgesetzt („Einfallswinkel gleich Ausfallswinkel“5). So ergeben sich diese beiden möglichen Lösungen:
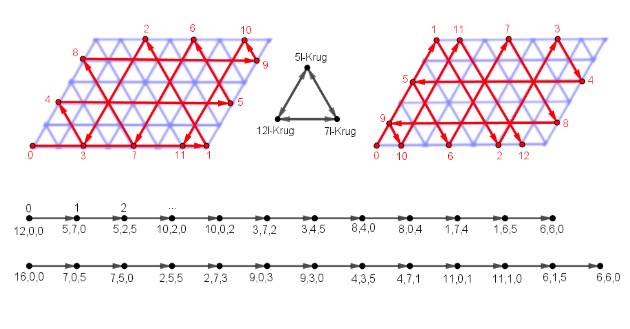
-
Strategiespiele zur Vertiefung
In Nr. 4 wurde ein besonders einfaches Spiel ausgewählt, um die ungewohnte Darstellung als Graph nicht zu überfrachten. Es wurde auf dem Arbeitsblatt eingebunden, da es sich auch für einen spielerischen Einstieg oder Ausklang eignet. Anspruchsvollere „Nimspiele“ und andere Strategiespiele bieten zahlreiche Anknüpfungspunkte zur weiteren Vertiefung.
Hierzu abschließend noch drei Anregungen6), die aufgrund ihres Motivationsgrades sicherlich auch in einer Weihnachtsstunde Verwendung finden könnten:
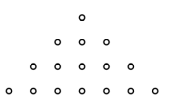
Nim 16 Spielsteine (z.B. Münzen) liegen wie zu sehen im Dreieck. Jeder darf aus einer der waagrechten Reihen 1,2 oder 3 Steine nehmen, die aber nebeneinander liegen müssen. Es wird abwechselnd gezogen, wer den letzten Stein nehmen muss, hat verloren.
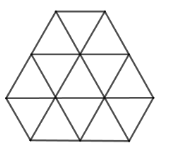
Nimbi (von Piet Hein): Auf jedem Schnittpunkt liegt eine Münze, die zu drei Reihen gehört, einer waagrechten und zwei diagonalen. Die Spieler nehmen sich abwechselnd aus einer Reihe so viele (ohne Lücke) nebeneinander liegende Münzen wie sie möchten (mindestens eine, höchstens alle). Wer die letzte Münze nehmen muss, hat verloren. Eine sichere Gewinstrategie zu Nimbi ist nicht bekannt.
Sprouts7(„Rosenkohl“)
Das Spiel für zwei Spieler startet im einfachsten Fall mit zwei beliebigen Punkten, die nach folgenden Regeln zu einem Graphen ausgebaut werden dürfen:
- Die Spieler verbinden abwechselnd zwei schon vorhandene Punkte durch eine beliebige Linie oder einen Punkt mit sich selbst durch eine Schleife und zeichnen anschließend auf die Linie bzw. Schleife einen neuen Punkt.
- Überschneidungen von Linien sind verboten.
- Von keinem Punkt dürfen mehr als 3 Striche ausgehen.
- Gewonnen hat der, der als letzter einen Zug ausführen kann.
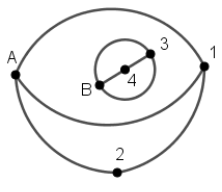
Das Bild zeigt das Ende eines möglichen Spieles, die beiden Startpunkte A und B waren vorgegeben. Von den Punkten A ,B , 1 und 3 gehen drei Striche aus, sie dürfen nicht weiter verwendet werden. Die Punkte 2 und 4 hätten zwar noch einen Strich „frei“, können aber nicht ohne Überschneidungen der Kanten verbunden werden. Der zweite Spieler hat gewonnen, da er als letzter die Punkte B und 3 verbunden und Punkt 4 auf die Linie gezeichnet hat. Der Reiz des Spiels liegt u.a. in der Verwendung von Schleifen, um die Verbindbarkeit einzuschränken. Schülerinnen und Schüler können die Gewinnstrategie für den 2. Spieler entdecken oder erarbeiten. Spieler 1 hat prinzipiell drei Möglichkeiten zur Eröffnung:
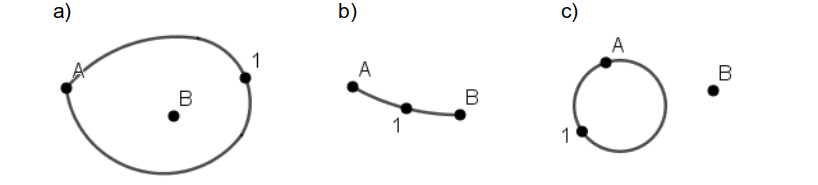
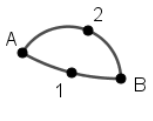
Bei a) verbindet Spieler 2 die Punkte A und 1 miteinander, Spieler 1 kann dann nur noch bei B eine Schleife zeichnen. Wie im oben kann Spieler 2 dann die Punkte B und 3 verbinden. Bei b) verbindet Spieler 2 die Punkte A und B wie skizziert. Alle vier Punkte haben nun noch einen Strich frei. Spieler 1 wird also zwei der Punkte innerhalb (oder außerhalb) des Gebiets verbinden, worauf Spieler 2 die anderen beiden Punkte außerhalb (bzw. innerhalb) verbindet und gewinnt. Bei c) verbindet Spieler 2 die Punkte A und 1. Spieler 1 muss dann eine Schleife bei B zeichnen und Spieler 2 geht wie bei der Schleife an A vor und gewinnt.
Die Schülerinnen und Schüler werden die Strategie nicht innerhalb einer Schulstunde finden, daher wird von E. Wittmann empfohlen, stärker zu lenken und nach der Erarbeitung der drei Eröffnungsvarianten in der Diskussionsphase jeweils die günstigsten Züge von Spieler 2 vorzugeben, die dann analysiert werden, um die Gewinnstrategie zu entwickeln.
Anregungen zur Vertiefung:
- Begründen lassen, dass das Spiel nach spätestens 5 Zügen beendet ist.
- Mit 3 statt 2 Punkten beginnen (dann ist das Spiel nach spätestens 8 Zügen beendet).
1 Ein Graph heißt Digraph (von directed - gerichtet), wenn jede seiner Kanten nur in einer bestimmten Richtung durchlaufen werden darf.
2 Erwein Flachsel: „Hunderfünfzig Mathe-Rätsel“, Klett-Verlag, Stuttgart, 1982, S.113
3 z.B. aus dem Unterstufenwettbewerb „Problem des Monats“: „Falsche Wahrheiten“ von Mai 2016
4 siehe Hintergrund. Weitere Informationen sind auch über die Weblinks auf der Seite https://de.wikipedia.org/wiki/Umfüllrätsel zugänglich (abgerufen am 13.4.2018).
5 Als Einfalls- bzw. Ausfallswinkel werden in der Physik die Winkel zwischen Strahl und Lot (Orthogonale zur Kante im Auftreffpunkt) bezeichnet, wogegen beim Billiard eher der Winkel von Strahl und Kante im Fokus steht.
6 Vgl. Anne Hilgers (Red.): „Spielen und Knobeln mit der Mathewelt“, Friedrich-Verlag, 2004, S. 12
7 Vgl. Erich C. Wittmann: „Punkte und Linien – 3 Ideen für Einzelstunden“, in Mathematik lehren 10, 1985, S. 45-47, Wittman bezieht sich dabei auf Martin Gardner: „Mathematical Games. Of sprouts and Brussels sprouts, games with a topological flavour,“ Scientific American 217 (July 1967), S. 112-115
6. Stunde: Wem gehört der Fisch? Logikrätsel und Tabellen
| Ablauf und Inhalte | Hinweise |
|
Fokus: Tabellen als heuristisches Hilfsmittel
|
|
Erläuterungen
In dieser Stunde sollen die Schülerinnen und Schüler Tabellen zur Lösung von bestimmten Logikrätseln verwenden und deren Nutzen erkennen. Folgendes bewusst einfach gehaltene Rätsel könnte dabei zu Stundenbeginn zur kognitiven Aktivierung genutzt werden:
Nachbarn
Martha, Gerd und Nele sind Nachbarn, ihre Häuser stehen nebeneinander in einer Reihe. Bestimmt die Farbe von Gerds Haus unter den folgenden Bedingungen:
(1) Das rote Haus steht links vom gelben Haus.
(2) Martha wohnt links von Gerd, das grüne Haus steht rechts von Nele.
(3) Gerd wohnt rechts des grünen Hauses.
Ihre Schülerinnen und Schüler könnten so argumentieren:
Das grüne Haus befindet sich in der Mitte, denn es steht rechts von Nele (2.) und links von Gerd (3.) Im grünen Haus muss demnach Martha wohnen. Da das rote Haus links vom gelben Haus steht (1.), ergibt sich folgende Konstellation von links nach rechts: Nele / rot, Martha / grün und Gerd / gelb. Zu erwarten ist auch der Einsatz einer Tabelle bei der Lösungsfindung.
Falls dies nicht von Seiten der SuS erfolgt, sollte nach der Präsentation einer Schülerlösung eine Tabelle zur unterstützenden Visualisierung erstellt werden, z.B.:

An dieser Stelle kann die Klasse festlegen, wie die Reihenfolge der Argumentation dokumentiert werden soll, z.B. durch eine vorangestellte Nummerierung der Einträge wie oben. Das im Zentrum stehende Einsteinrätsel könnte auch direkt gestellt werden. Im Stundenentwurf wurde allerdings eine inhaltliche Vorbereitung durch Aufgabe 1 geplant, indem die Verwendung einer Tabelle reflektiert und bestimmte Argumentationsmuster exemplarisch beleuchtet werden. Für beide Rätsel stehen Präsentationen im opd-Format zur Verfügung. Auf dem ergänzenden Übungsblatt steht ein dem Einsteinrätsel nachempfundenes Logikrätsel mit nur jeweils vier Merkmalen zur Verfügung, das ebenfalls zum Einstieg genutzt werden könnte.
Es folgen Anmerkungen zu den einzelnen Aufgaben.
Drei Freundinnen
Die in der Musterlösung gewählte Argumentation dürfte den meisten Schülerinnen und Schülern naheliegen. Sie geht von den beteiligten Personen aus und betrachtet die weiteren Merkmale jeweils mit direktem Bezug zu den Personen. Es sollten aber auch andere Strategien exemplarisch verdeutlicht werden. Für das Einsteinrätsel ist z.B. ein Perspektivwechsel wie der folgende hilfreich:

1 steht fest, danach visualisiert man die Aussagen (1.) und (3.) als „Blöcke“, die hier jeweils übereinanderliegende Zellen belegen. (3.) kann dabei nicht zu Haus 1 gehören, da dort bereits Klavier gespielt wird. (1.) kann ebenfalls nicht zu Haus 1 gehören, da Anna links von Tina wohnen muss (4.). Damit müssen die markierten Blöcke also zu Haus 2 oder 3 gehören und es folgt mit Blick auf die Sportarten, dass für Haus 1 nur noch Handball in Frage kommt. Der zur Lösung erforderliche Perspektivwechsel lässt sich hier gut als Wechsel von der senkrechten zur waagrechten Sicht deuten. Zuerst sind die vertikal angeordneten Merkmale (z.B. „Tina macht Judo“) im Blick, bevor der Blick auf die horizontalen Beziehungen gelenkt wird, um nach dem Ausschlussprinzip die Sportarten-Zeile zu ergänzen. Mit der Datei 06_Drei_Freundinnen.odp kann der Perspektivwechsel besprochen werden.
Einsteinrätsel
Dieses wohl berühmteste Logikrätsel wird häufig Albert Einstein zugeschrieben, der gesagt haben soll, dass höchstens 2% der Weltbevölkerung in der Lage wären, es zu lösen. Es gibt allerdings keinerlei Hinweise auf den Verfasser oder eine Verbindung zu Albert Einstein. Das Rätsel wurde erstmals 1962 veröffentlicht, ca. 7 Jahre nach Einsteins Tod.
Ausführlichere und übersichtlichere Lösungen für das Einsteinrätsel werden im Internet angeboten und verwenden für neue Folgerungen jeweils neue Tabellen. Man benötigt so allerdings meist über 10 Tabellen, die dann als Blankokopiervorlage zur Verfügung gestellt werden müssten. Für die unterrichtliche Umsetzung erschien dies wenig praktikabel. Hier bietet sich eher die schrittweise Entwicklung in einer Tabelle (z.B. an der Tafel) an, wobei die einzelnen Folgerungen dann wie in der Musterlösung nummeriert und erläutert werden können. Im Internet werden auch Kreuztabellen als Lösungsvorlage für das Einsteinrätsel angeboten, deren Einsatz möglich wäre. Die eigentliche Aussagenlogik wird zwar durch das eher „schematische“ Abarbeiten in den Hintergrund gedrängt, durch die Nutzung von „Logiklösern“ könnten medienaffine SuS aber durchaus dazu angeregt werden, eigene Logikrätsel zu erstellen und zu überprüfen.9
Unabhängig vom gewählten heuristischen Hilfsmittel müssen die SuS letzlich bei der Lösungsfindung festgelegte Hürden meistern. Bei der in der Musterlösung gewählten Argumentationsreihenfolge sind es beispielsweise die noch leichteren Schritte 4 und 7, vor allem aber der erforderliche Perspektivwechsel bei Folgerung 12, bei dem man nach dem Ausschlussprinzip auf das Getränk in Haus 1 schließt. Man kann dabei nicht wissen, wie die Klasse vorankommt und wird ggf. mit dem nötigen Fingerspitzengefühl ergänzende lenkende Aufträge geben, die den jeweiligen Argumentationsschritt anbahnen. In der Regel sollte das Rätsel aber gut zu lösen sein. Zur Reflexion könnte auch die Datei 06_Einsteinraetsel.odp genutzt werden. Bei den Übungsaufgaben steht als Variante Aufgabe 1 („Im Kino“) mit vier beteiligen Personen zur Verfügung.
Studienorte
Bei diesem Rätseltyp geht es um zwei Hauptmerkmale (hier z.B. Name und Studienort) und ein untergeordnetes aber wichtiges Hilfsmerkmal (hier das Studienfach). Die Tabelle dient ebenfalls als heuristisches Hilfsmittel zur Visualisierung der Folgerungen, damit der rote Faden nicht verloren geht. Da hier aber nur nach der Passung von Name und Studienort gefragt ist, genügen die Eintragungen „+“ bzw. „-“. Die einzelnen Folgerungen können auch wieder nummeriert und ergänzend erläutert werden. Bei den Übungsaufgaben wurden mit Aufgabe 2 und 3 weitere Rätsel dieser Art eingebunden, die z.B. auch als Hausaufgabe genutzt werden könnten.
Sudokus
Es wurde ergänzend ein leichtes Sudoku aufgenommen, da diese Rätselform sicherlich motivierend wirken kann. In Bezug auf universelle heuristische Hilfsmittel bietet sie allerdings weniger Potenzial als die ausgewählten Logikrätsel, mit denen die im Fokus stehende Aussagenlogik besser propädeutisch vorbereitet werden kann. Dennoch könnte dieses Sudoku als Ausgangspunkt für eine Vertiefung dienen, in der dann auch spezifische Lösestrategien beleuchtet werden könnten.10
Da davon auszugehen ist, dass einige Schüler die Regeln kennen und diese der Klasse erläutern können, wurde auf dem Blatt auf die Auflistung verzichtet. Der Vollständigkeit halber seien sie hier kurz genannt: Die Ziffern 1 bis 9 müssen so verteilt werden, dass jede Ziffer genau einmal in jeder Spalte, einmal in jeder Zeile und einmal in jedem der der neun kleinen Quadrate vorkommt.
Logikrätsel in kooperativen Übungsphasen
Ausdrücklich empfohlen wird das „Gewürzregal“ (Datei 07_aug_ab_Gewürzregal.odt) - ein Logikrätsel aus Schleswig-Holstein, dessen Bearbeitung in besonderem Maße kommunikative Kompetenzen fördert. Es wurde nach der Idee eines namentlich nicht mehr ermittelbaren Kollegen am Institut für Qualitätsentwicklung an Schulen Schleswig-Holstein (IQSH) entwickelt und wird von Herrn Helmut Mallas zur nicht-kommerziellen Nutzung zur Verfügung gestellt.11
Daneben bieten sich auch kommerzielle Logikrätselsammlungen an, die im Unterricht als Aufgabenpool für kooperative Übungsphasen genutzt werden könnten.12
8 Vgl. z.B. Hans J. Schmidt: „Prof. Dr. Brian Teaser´s Denk-Mal-Rätsel“, Aulis-Verlag, Köln, 2009 oder „Prof. Dr. Brian Teaser im Sudoku-Fieber“, Aulis-Verlag, Köln, 2006
9 z.B. Logiklöser von J. Singler, URL: http://www.jsingler.de/apps/logikloeser (abgerufen am 8.5.2018).
10 Eine lesenswerte Sammlung verschiedener Sudoku-Strategien von Wolfgang Urban findet man unter http://www.hib-wien.at/leute/wurban/mathematik/sudoku_strategie.pdf (zuletzt abgerufen am 19.4.2018).
11 Herr Mallas stellt seine reichhaltige Materialsammlung für die nicht-kommerzielle Nutzung im Bildungsbereich zur Verfügung, Kontakt per email: (Anfrage auch möglich an: )
12 z.B. „Think-Logik-Rätsel“ bzw. „Think - noch mehr Logik-Rätsel“ des Ravensburger-Verlages
7. Stunde: Wiederholung „Kreuz und quer“
| Ablauf und Inhalte | Hinweise |
|
kooperative binnendifferenzierende Wiederholungsstunde
|
|
Erläuterungen
Diese Wiederholungsstunde soll einen motivierenden Abschluss ermöglichen, bei dem die verschiedenen erworbenen Kompetenzen angewendet werden können. Zu zentralen Inhalten der Einheit wurden hierzu die Aufgaben 1-7 konzipiert.
Aufgabe 8 bietet darüber hinaus die Möglichkeit, geometrische Aspekte in den Vordergrund zu stellen und so zur Geometrieeinheit überzuleiten, falls sich diese anschließen sollte. Als differenzierender Zusatzauftrag wurde der b)-Teil aufgenommen, bei dem flexible dynamische Vorstellungen zur Lösung erforderlich sind. Diese Aufgabe lässt sich sehr gut variieren und kann die SuS auch zu eigenen Untersuchungen anregen.13
Für Aufgabe 5 steht die Datei 07_aug_ab_wiederholung_Nr5_loesung.ggb zur Visualisierung der Hamilton-Kreise bzw. Sitzordnungsreihenfolgen zur Verfügung. Bei Aufgabe 6 wurde auch die graphische Lösungsfindung mithilfe des Kantenzugs im Billiardgraphen“ eingebunden. Bei Bedarf kann die Datei 07_aug_ab_wiederholung_Nr6_loesung.ggb zur Erläuterung der beiden Lösungen in 7 bzw. 18 Umfüllvorgängen eingesetzt werden.
13 Esther Schmitt: „Knobel-Aufgaben für die 5. und 6. Klasse“ Reihe EinsPlus., Cornelsen Scriptor, 2004, S.68 vgl. auch Erich C. Wittmann: „Wer macht die meisten Schnittpunkte?“, in: „Punkte und Linien – 3 Ideen für Einzelstunden“, Mathematik lehren 10, 1985, S. 45-47
Unterrichtsverlauf: Herunterladen [odt][407 KB]
Unterrichtsverlauf: Herunterladen [pdf][435 KB]
Weiter zu Literatur