Gruppe 3: Rechtecke mit Quadraten auslegen
In dieser geometrischen Methode zur Bestimmung desggT zweier Zahlen , startet man mit einem Rechteck, dessen Seitenlängen genau diesen beiden Zahlen entsprechen. In der Abbildung wurden die Seitenlängen 26 und 16 gewählt.

Schritt 1
Man zeichnet nun ein möglichst großes Quadrat so in das Rechteck, dass eine zusammenhängende Fläche übrig bleibt. Zum Beispiel so:
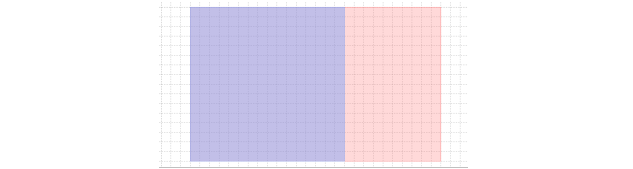
Schritt 2
Wenn die zusammenhängende Restfläche ein Quadrat ist, so ist der gesuchte ggT dessen Seitenlänge. Ansonsten führt man Schritt 1 erneut in der Restfläche durch.
*Und noch eine Bemerkung zum Schluss:
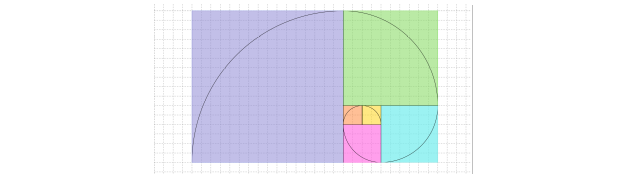
Manchmal ergeben sich Unterteilungen, bei denen man in die entstandenen Quadrate Viertelkreise so einzeichnen kann, dass sich eine hübsche Spirale ergibt. Wann ist dies der Fall? Versuche es, selbst herauszufinden. Ein Tipp: Es hat etwas mit den sogenannten Fibonacci-Zahlen zu tun. Mehr dazu kannst du auch im Internet finden.
Der Euklidische Algorithmus: Herunterladen [odt][466 KB]
Der Euklidische Algorithmus: Herunterladen [pdf][857 KB]
Weiter zu Lösungen
