Re­chen­ver­fah­ren – Lö­sun­gen

Auf­trä­ge in Part­ner­ar­beit:

Quel­le: ZPG IMP

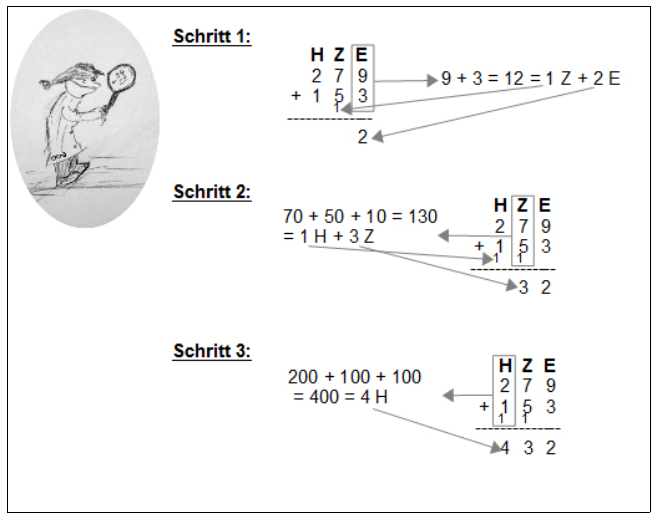
1. In der Ab­bil­dung oben ist das schrift­li­che Re­chen­ver­fah­ren zur Ad­di­ti­on mit­hil­fe des Über­tra­ges an einem aus­führ­li­chen Bei­spiel dar­ge­stellt.

   a.) Über­tragt das Ad­di­ti­ons­ver­fah­ren auf das Bi­närs­ys­tem, be­rech­net und no­tiert dazu in ver­gleich­ba­rer Art und Weise die Ad­di­ti­on 1012 + 112 .

   

   b.) Be­rech­net mit­hil­fe die­ses Ad­di­ti­ons­ver­fah­rens die fol­gen­den Sum­men:

   

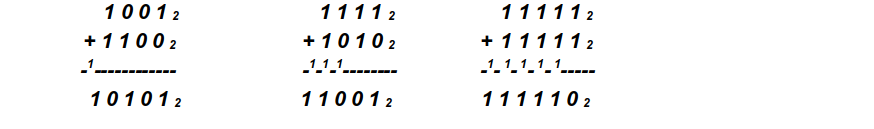
2. Ihr sollt nun ein wei­te­res, euch im de­zi­ma­len Stel­len­wert­sys­tem be­kann­tes schrift­li­ches Re­chen­ver­fah­ren auf das Bi­närs­ys­tem über­tra­gen. Wählt dazu min­des­tens eine der fol­gen­den Auf­ga­ben aus:

   • Sub­trak­ti­on:

     Führt die schrift­li­che Sub­trak­ti­on 31 – 13 schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und sub­tra­hiert 11011₂ – 1101₂

   Vor­be­mer­kung: Für die schrift­li­che Sub­trak­ti­on gibt es ver­schie­de­ne Re­chen­ver­fah­ren. Im fol­gen­den Ab­schnitt wird das Er­gän­zungs­ver­fah­ren be­schrie­ben. Falls das in Klas­se 5 / 6 in Ma­the­ma­tik ein­ge­führ­te Schul­buch ein an­de­res Ver­fah­ren ver­wen­det, soll­te die Lö­sung ent­spre­chend an­ge­passt wer­den.

   

   • Di­vi­son ohne Rest

     Führt die schrift­li­che Di­vi­si­on 465 : 15 schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und di­vi­diert 1100₂ : 10₂

     Die Di­vi­si­on funk­tio­niert eben­so wie im De­zi­mal­sys­tem. Hier­in wird eine „in­tui­ti­ve Sub­trak­ti­on“ be­nö­tigt, falls man diese noch nicht durch­drun­gen hat.

   

   • Mul­ti­pli­ka­ti­on

     Führt die schrift­li­che Mul­ti­pli­ka­ti­on 123 · 72 schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und mul­ti­pli­ziert 11011₂ · 1011₂

   

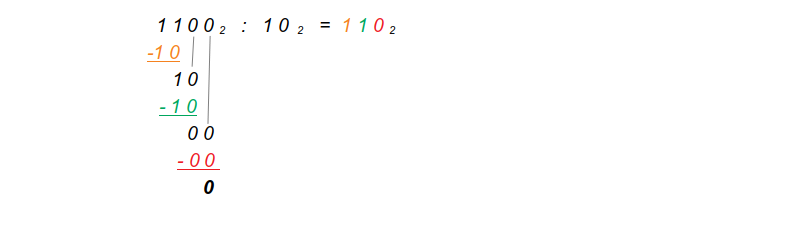
   Um­gangs­sprach­lich kann man die Mul­ti­pli­ka­ti­on so cha­rak­te­ri­sie­ren: Wenn eine Zahl a mit einer Zahl b in Bi­när­dar­stel­lung mul­ti­pli­ziert wird, dann schreibt man für jede Zif­fer 1 an be­lie­bi­ger Stel­le k in b die Zahl a er­neut auf, und hängt k-1 Nul­len an. All diese Zah­len wer­den dann zum Er­geb­nis a · b auf­ad­diert. Im Bei­spiel von oben:

   

   • (**) Zu­satz­auf­ga­be: Di­vi­si­on mit Rest

     Führt die schrift­li­che Di­vi­si­on für 123 : 7 mit Rest schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und di­vi­diert 1011₂ : 11₂

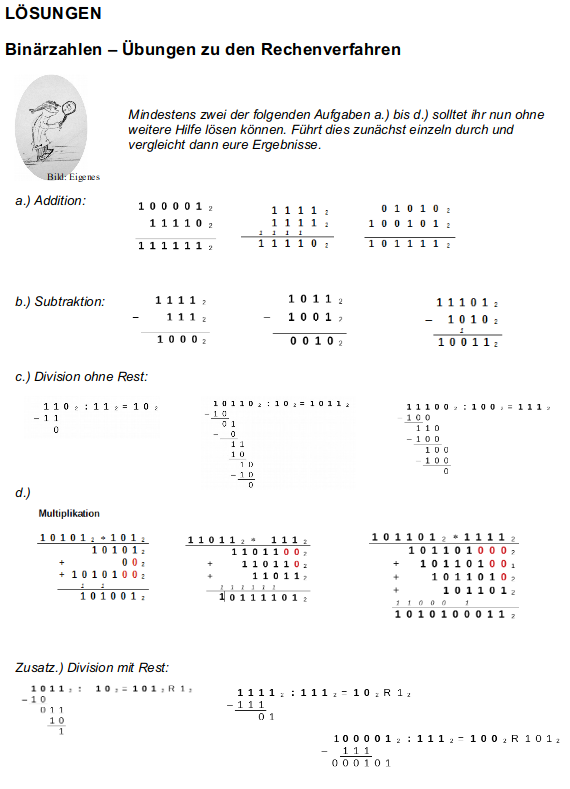
Bi­n­är­zah­len – Übun­gen zu den Re­chen­ver­fah­ren

Re­chen­ver­fah­ren - Lö­sun­gen, Seite 5 von 5

Re­chen­ver­fah­ren – Lö­sun­gen: Her­un­ter­la­den [odt][365 KB]

Re­chen­ver­fah­ren – Lö­sun­gen: Her­un­ter­la­den [pdf][214 KB]

Wei­ter zu He­xa­de­di­mal­zah­len