Sie sind hier:

Das XO-Spiel

Das XO-Spiel geht auf die Idee von Jens Gallenbacher¹ zurück. Das, was hierbei als „Zauberei in der Informatik“ gezeigt wird, beinhaltet eine sehr schöne Erklärung der Begriffe „Redundanz von Informationen“, „Fehlerkorrekur“ und „Fehlererkennung“. Man benötigt für dieses Spiel lediglich beidseitig beschriftete Kärtchen, wobei eine Seite eines Kärtchens mit dem Symbol „X“ und die andere Seite mit dem Symbol „O“ gekennzeichnet ist. Eine Kopiervorlage findet man unter 02_kopiervorlagen/02_duc_kopiervorlage_xo_spiel.pdf. Idealerweise werden die X- und O-Kärtchen auf unterschiedlich farbigem Papier gedruckt und anschließend zusammen mit Vorder- und Rückseite laminiert. Auch im Buch von Jens Gallenbacher, Abenteuer Informatik, ist im Anhang eine kartonierte Vorlage zu finden. Benötigt werden mindestens 36 solcher Kärtchen. Hat man mehr dieser Kärtchen, lässt sich die „Zauberei“ etwas überzeugender durchführen. In der Arbeitsphase bekommt jede Gruppe ein solches Kartenset. Zum Vorführen vor der gesamten Gruppe eignen sich auch Wendemagnete, die an Tafeln haften bleiben. Diese können im Internet bestellt werden.

1. Ablauf des Spiels

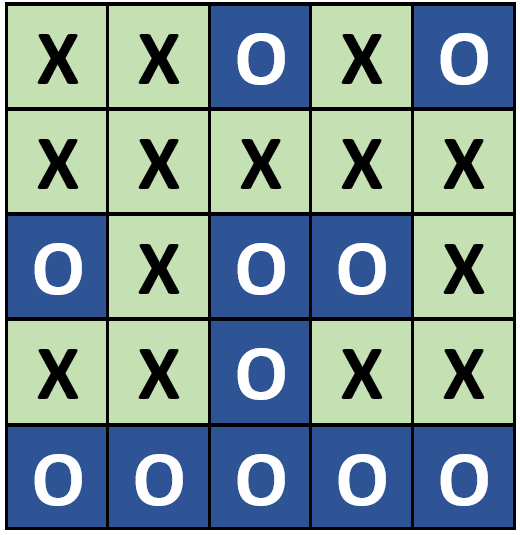
Abb. 1: 5x5-Ausgangsmuster

Der „Zauberer“ (beim ersten Vorführen dieses Spiels ist dies die Lehrkraft) gibt an, magische Fähigkeiten zu besitzen. Um dies demonstrieren zu können, bittet der Zauberer ein oder mehrere Schülerinnen und Schüler mithilfe der Kärtchen ein beliebiges, möglichst kompliziertes 5x5-Muster zu legen. Dabei sieht er absichtlich nicht genau zu, was gelegt wird. Er behauptet, er könne anschließend mithilfe seiner magischen Kräfte jedes geheim umgedrehte Kärtchen finden, ohne sich das Muster vorher einprägen zu müssen. Zum Beispiel könnte das von den Schülerinnnen und Schülern gelegte Muster wie in Abb. 1 aussehen. Der Zauberer beschließt spontan, den Schwierigkeitsgrad des Spiels zu erhöhen und – damit es angeblich etwas schneller geht – ergänzt selber rasch und scheinbar zufällig das gelegte Muster zu einem 6x6-Muster.

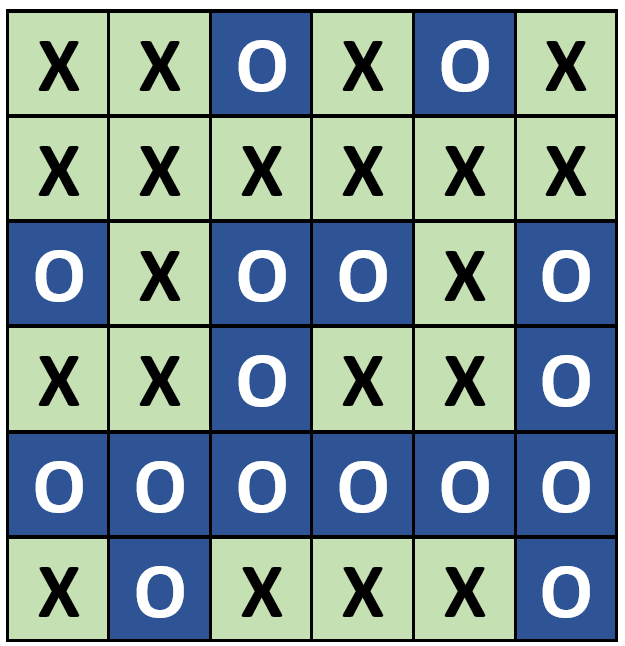
Abb. 2: 6x6-Muster

Beispielsweise wird jeweils rechts und unten eine Spalte bzw. Zeile ergänzt (vgl. Abb. 2). Der Zauberer bittet nun, dass heimlich eine Karte umgedreht werden soll. Er selber dreht sich dabei mit dem Rücken zum Spiel oder verlässt kurz den Raum. Dann kehrt er zurück zum Spiel und lässt seine Magie spielen – und findet die umgedrehte Karte! Um die Glaubwürdigkeit des Zauberers zu unterstreichen, kann das Spiel wiederholt werden.

2. Fehlererkennung und Fehlerkorrektur (1-bit, 2-bit, 3-bit-Fehler)

Gemeinsam oder in kleineren Gruppen soll nun der Zaubertrick gelüftet werden. Die Idee, die hinter diesem Trick steckt, ist, dass das Legen der scheinbar zufälligen Karten zu einem 6x6-Muster einer strikten Regel folgt. Jede Zeile und jede Spalte wird so ergänzt, dass die Anzahl der „X“-Karten und die Anzahl der „O“-Karten in allen Zeilen und Spalten stets gerade ist.

Die XO-Karten können natürlich auch binär interpretiert werden. Ein X entspricht dabei einer 1, ein O entspricht einer 0. Es liegt nun die Frage auf der Hand, ob sich der Informationsgehalt der zunächst gelegten 25 Karten nach dem Ergänzen zu einem 6x6-Muster mit 36 Karten auch erhöht hat. Die Antwort ist: nein. Denn man kann jederzeit die zusätzlichen Karten wieder wegnehmen und die ursprüngliche Information bleibt erhalten. Genauso kann auch jederzeit das Muster nach der vorgegeben Regel wieder ergänzt werden. Man kann feststellen, dass sogar jede beliebige Spalte und jede beliebige Zeile entfernt werden kann, um daraus wieder eindeutig das Muster zu ergänzen. Hierbei lässt sich der Begriff der „Redundanz“ erklären. Die zusätzlichen Karten (in der Informatik entsprechen diese den Bits) ändern den Informationsgehalt nicht.

Damit stellt sich aber nun die Frage, wozu man dann diese zusätzlichen Karten (Bits) benötigt. Dieser Fragestellung soll nun im Folgenden und mithilfe des Arbeitsblattes (02_duc_ab_xo_spiel.odt) nachgegangen werden.

In Partnerarbeit oder in Kleingruppen kann das Arbeitsblatt von den Schülerinnen und Schülern erarbeitet werden. Nachdem in den Gruppen das Spiel selbstständig und mit unterschiedlichen 5x5-Ausgangsmustern durchgeführt wurde, sollen nun zu einem nicht mehr zu ändernden 6x6-Muster entsprechende Fragen gelöst werden.

Das Ziel dabei ist, dass die Schülerinnen und Schüler feststellen, dass mithilfe der Redundanzen manche Fehler erkannt werden können. In bestimmten Fällen kann ein Fehler nicht nur erkannt, sondern sogar korrigiert werden. Auf den Arbeitsblättern sollen die Schülerinnen und Schüler diejenigen Positionen in den vorgedruckten Rastern farbig markieren, die jeweils für die Lösung der Aufgabe relevant sind, vergleichbar mit den Abbildungen 3 bis 7.

Der erste Fall entspricht dem oben durchgeführten Zauberspiel. Egal wie das 5x5-Ausgangsmuster gelegt und nach der vorgegeben Regel zu einem 6x6-Muster ergänzt wurde, es lässt sich an jeder Position eine falsch gelegte Karte finden und durch Umdrehen korrigieren. Das bedeutet, dass hierbei 1-bit-Fehler stets erkannt und korrigiert werden können.

1-bit Fehler sind fehlererkennend und fehlerkorrigierend.

Im zweiten Fall soll überprüft werden, ob sich auch 2-bit-Fehler, also das Umdrehen von zwei Karten, ebenfalls finden und korrigieren lassen. Bei dem 6x6-Muster aus Abb. 2 werden nun hierfür zwei beliebige Karten umgedreht. Diese sind in der Abb. 3 mit einem roten Rahmen markiert. Man kann nun feststellen, dass sowohl in der 2. und 5. Zeile als auch in der 2. und 4. Spalte die Anzahl der X-Kärtchen und die Anzahl der O-Kärtchen nicht mehr gerade ist. Man weiß nun also, dass in der Tat zwei Fehler vorliegen. Das bedeutet, dass Fehlererkennung bei zwei falschen Bits möglich ist. Lässt sich dieser 2-bit-Fehler aber auch korrigieren? Dies wird in der Abb. 4 verdeutlicht. Es gibt nämlich zwei mögliche Paare von Bits, die für eine Korrektur infrage kommen, sodass nach deren Umdrehen die geforderte Regel wieder eingehalten wird: das rote Pärchen und das gelbe Pärchen. Die vier Bits bilden zusammen die Ecken eines Rechtecks. Somit kann es also passieren, dass bei einem 2-bit-Fehler falsch korrigiert und damit alles verschlimmert wird.

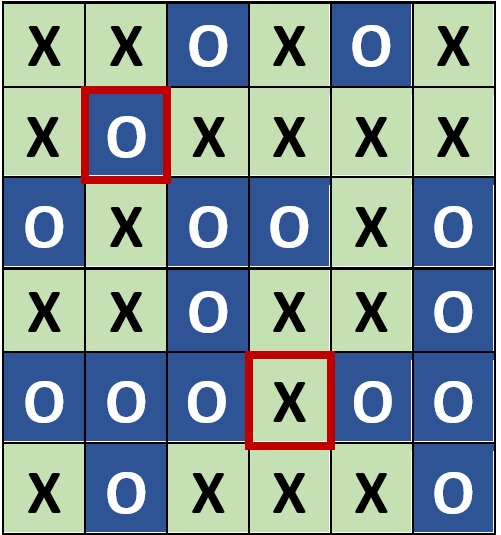
Abb. 3: 2-bit-Fehler

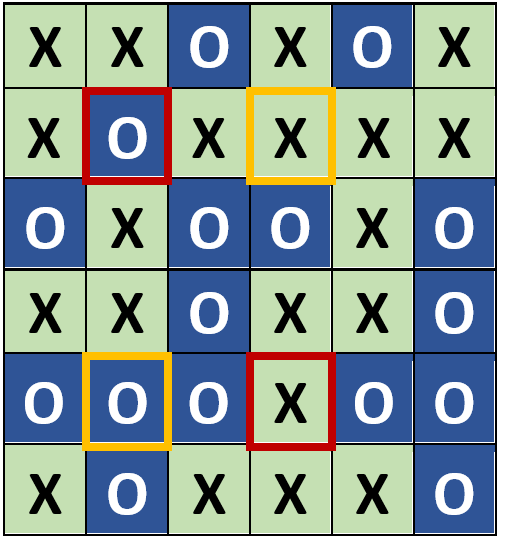
Abb. 4: 2-bit-Fehler

Werden zwei direkt nebeneinander liegende Kärtchen umgedreht, beispielsweise in einer Zeile, so kann man zwar in den beiden betreffenden Spalten erkennen, dass zwei Fehler vorliegen müssen, jedoch bleibt die Anzahl der X- und O-Kärtchen in der betroffenen Zeile gerade, so dass jede Zeile für eine Korrektur infrage kommen kann.

2-bit-Fehler sind fehlererkennend, jedoch nicht fehlerkorrigierend.

Im dritten Fall beschäftigt man sich mit 3-bit-Fehlern. Es können wieder verschiedene Szenarien durchgespielt werden, die sich darin unterscheiden, wo die fehlerhaften Bits im Muster verteilt sind. Ein Szenario wird in den Abbildungen 5 und 6 gezeigt. Wieder sind die fehlerhaften Bits rot markiert. In den Spalten 2, 3 und 5 sowie in der Zeile 2 wird die Regel verletzt. Eine Vermutung könnte sein, dass somit die Fehler gefunden und korrigiert werden können. Jedoch zeigt die Abbildung 6 ebenfalls ein fehlerhaftes Muster, wieder in den Spalten 2, 3 und 5 und in der Zeile 2. Offensichtlich ist dies aber ein anderer Fehler.

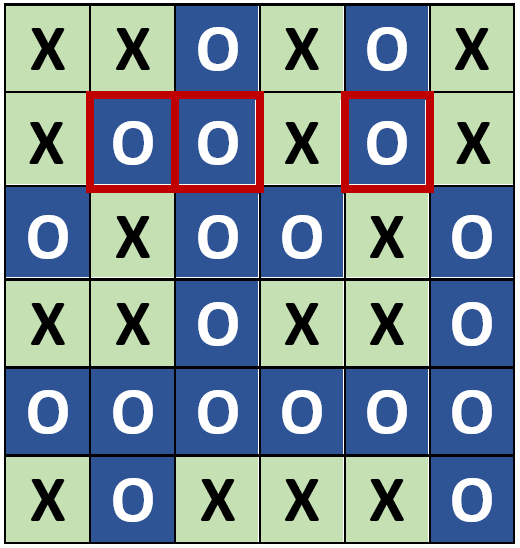
Abb. 5: 3-bit-Fehler

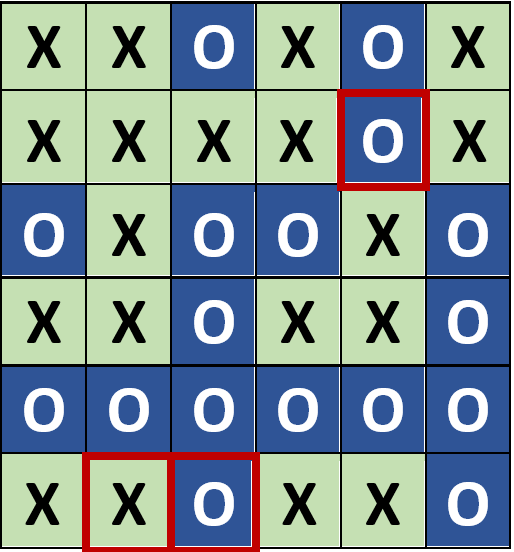
Abb. 6: 3-bit-Fehler

Somit ist klar, dass dieses fehlerhafte Muster nicht korrigiert werden kann. Der 3-bit-Fehler ist in diesem Fall erkennend, aber nicht korrigierend.

Noch viel dramatischer zeigt sich das Szenario, das in Abb. 7 gezeigt wird. Die drei Fehler liegen so, dass sie drei Ecken eines Rechtecks bilden. Hier liegt zwar ein 3-bit-Fehler vor, er wird jedoch fälschlicherweise als 1-bit-Fehler erkannt und somit auch entsprechend falsch korrigiert (gelb umrandet). In diesem Fall wird der 3-bit-Fehler als solcher gar nicht erkannt.

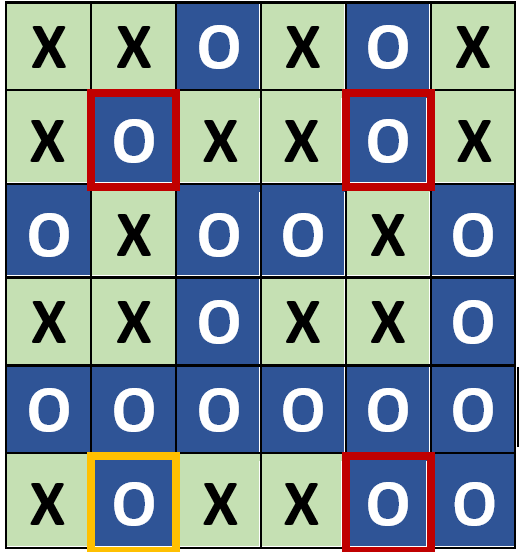
Abb. 7: 3-bit-Fehler

Zusammengefasst kann man daher sagen:

Will man Fehlerkorrektur betreiben, so können 1-bit-Fehler erkannt und korrigiert werden, 2-bit-Fehler können hingegen nur erkannt werden.
Nur wenn man auf die Fehlerkorrektur verzichtet, ist es möglich bis zu drei Fehler zu erkennen.

Als Zusatzaufgabe im Rahmen der Binnendifferenzierung kann überlegt werden, wie man mithilfe zusätzlicher Redundanzen die Zahl der korrigierbaren bzw. erkennbaren Fehler steigern könnte.

¹ Jens Gallenbacher, Abenteuer Informatik, Kapitel 11 „InformaGik“

Unterrichtsverlauf: Herunterladen [odt][408 KB]

Unterrichtsverlauf: Herunterladen [pdf][1 MB]

Weiter zu Das Sender-Empfänger-Spiel