Gruppe 2: Schere und Papier

Den ggT eines Zahlenpaares kann man auch mit Schere und Papier schrittweise an einem Rechteck herausfinden. Das Rechteck muss dabei zunächst die Seitenlängen des Zahlenpaares aufweisen, also beispielsweise 24 Kästchen lang und 9 Kästchen breit, wenn man den ggT(24; 9) bestimmen möchte. Also so:

Schritt 1

Man legt das Rechteck so vor sich hin, dass die Breite größer ist als die Höhe. Dies ist im oberen Beispiel schon gemacht. Nun faltet man die Ecke links oben auf die untere Kante und schneidet den überlappenden Teil (in Form eines Dreiecks) ab. Dieser ergibt aufgefaltet ein Quadrat, welches wir weglegen. Übrig bleibt entweder ein Quadrat oder ein „normales“ Rechteck.

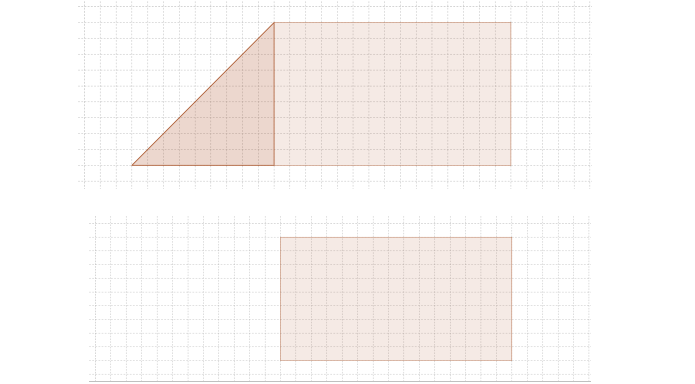
Schritt 2

Wenn man nun ein Quadrat vor sich liegen hat, dann misst man dessen Seitenlänge ab. Diese Länge ist der gesuchte ggT. Falls das übrig gebliebene Rechteck kein Quadrat ist, führt man Schritt 1 erneut durch.

Der Euklidische Algorithmus: Herunterladen [odt][466 KB]

Der Euklidische Algorithmus: Herunterladen [pdf][857 KB]

Weiter zu Gruppe 3