Multigraphen – Übungen – Lösung

1. Multigraphen, Eulersche Kantenzüge

   

   a) bis d) sind Multigraphen, da sie Mehrfachkanten besitzen, meist Doppelkanten.

   e) ist ein einfacher Graph. Alle Graphen außer d) besitzen nur Knoten gerader Ordnung und sind daher eulersch, es existieren also bei a)-c) und e) geschlossene Eulersche Kantenzüge.

   Bei d) gibt es offene Eulersche Kantenzüge mit den markierten Start- bzw. Endknoten.

2. Eulersche Kantenzüge

   Nach dem Bau der 8. (bzw. 9.) Brücke waren Stadtspaziergänge möglich, bei denen man jede der 8 (bzw. 9) Brücken genau einmal überquerte. Nach dem Bau der 8. Brücke konnte man auf der Insel beginnen und endete im Osten (oder umgekehrt). Nach dem Bau der 9. Brücke konnte man auch auf der Insel beginnen, endete aber im Süden (oder umgekehrt). Ein echter Rundgang mit Rückkehr zum Ausgangspunkt war nicht möglich (Die Graphen enthalten genau zwei ungerade Knoten, es existieren „nur“ offene Eulersche Kantenzüge).

3. Wohnungsrundgang

   

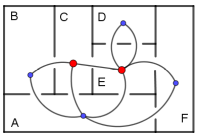
   Mit einem Graphen lässt sich das Problem übersichtlich darstellen. Man fasst die Räume als Knoten und die Türen als Kanten auf. Der Graph hat genau zwei ungerade Knoten (Raum C und E), d.h. es gibt offene Eulersche Kantenzüge. Der „Wohnungsrundgang“ kann nur in C beginnen und endet dann in E oder umgekehrt. Ein möglicher Rundgang wäre z.B. CBACEAFEDE.

4. Briefträgerproblem

   

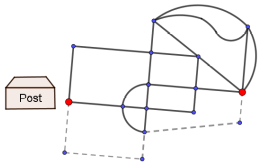
   Es ist möglich. Fasst man die durchgezogenen Linien als Kanten und die Schnittpunkte als Knoten eines Graphen auf, erkennt man, dass alle Knoten die Ordnung 2 oder 4 besitzen, der Graph also eulersch ist. Wenn die gestrichelten Linien als Kanten hinzukommen, entstehen die beiden markierten ungeraden Knoten, die dann Start- und Endknoten sein müssen. Der Briefträger muss dann einige Straßenzüge doppelt ablaufen, um wieder zur Post zurückkehren zu können.

5. Schneepflug

   

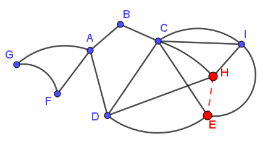
   a) Ja, es ist möglich. Alle Knoten im Netz haben gerade Ordnung. Daher existiert mindestens ein Eulerscher Kantenzug, den der Fahrer als Fahrtroute nutzen kann, z.B. BCIHEDAFGAB.

   b) Falls die Straße von E nach H aber gesperrt ist, so reduziert sich die Ordnung beider Knoten um 1 und ist damit ungerade. Dann existiert kein Eulerscher Kantenzug, der in B startet.

Multigraphen – Übungen – Lösung: Herunterladen [odt][280 KB]

Multigraphen – Übungen – Lösung: Herunterladen [pdf][239 KB]

Weiter zu andere Reihenfolge