Beweis 2

¹

Idee: Betrachtung der Abstände als Höhen geeigneter gleichseitiger Dreiecke

Datei: 03_geo_viviani_Beweis_II.ggb

Vor.: ABC ist ein gleichseitiges Dreieck, P ist ein Punkt im Innern oder auf dem Rand des Dreiecks ABC. Die Abstände von P zu den drei Seiten werden mit r, s, t bezeichnet, h ist die Höhe des Dreiecks.

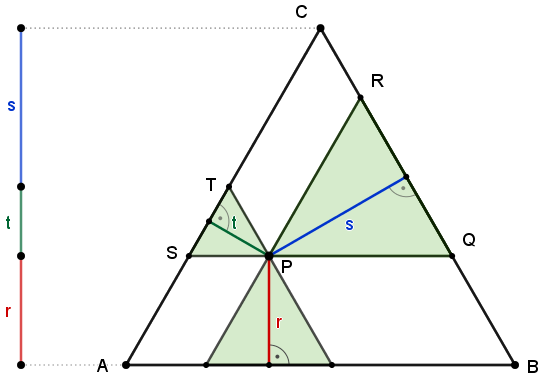
z.z.: r + s + t = h

Die Parallelen zu den Dreiecksseiten durch P bilden zusammen mit den Seiten des Dreiecks ABC drei Teildreiecke und drei Parallelogramme, die hier grün bzw. weiß gefärbt sind.

Alle Innenwinkel der grünen Teildreiecke sind 60° weit, da sie als Stufen- bzw. Wechselwinkel an parallelen Geraden mit den Winkeln des Dreiecks ABC übereinstimmen. Die Teildreiecke sind gleichseitig.

Nun ordnet man die Dreiecke geschickt um, so dass die Summe ihrer Höhen der Höhe h des Dreiecks ABC entspricht. Man verschiebt dazu z.B. das Dreieck PQR parallel zur Seite BC, bis für das verschobene Dreieck P*Q*R* gilt: R*=C, bis also die Ecke R* im Punkt C liegt. Dann gilt auch P*=T, da PRCT ein Parallelogramm ist mit PT=RC:

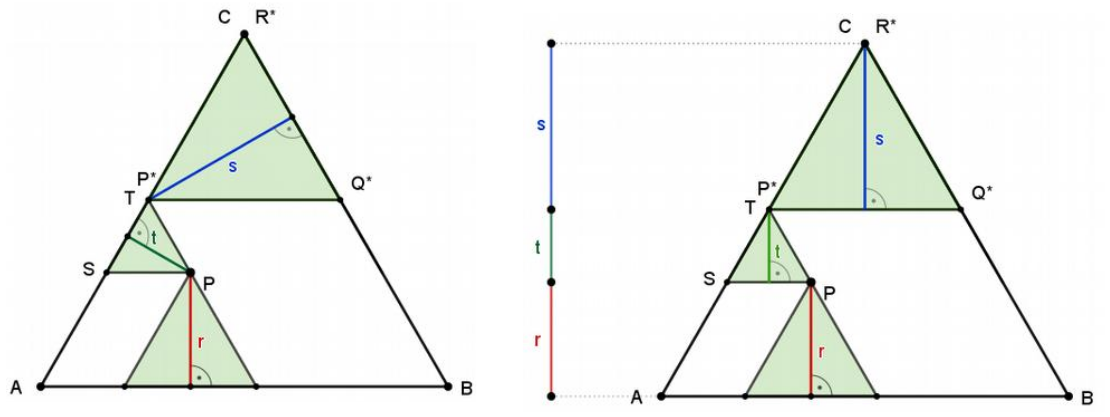
Da in einem gleichseitigen Dreieck die drei Höhen gleich lang sind, kann man in den beiden oberen Dreiecken andere Höhen mit gleicher Länge einzeichnen. Alternativ könnte man die Dreiecke auch um 60° drehen. Da T=P* und AB || SP || P*Q* , ergibt die Summe der Höhen der drei Dreiecke die Gesamthöhe des Dreiecks ABS, es gilt also r + s + t = h

Mit der genannten Datei lässt sich der Beweisgang dynamisch visualisieren, die Parallelverschiebungen können dabei animiert werden.

Satz von Viviani – Lösungen: Herunterladen [odt][414 KB]

Satz von Viviani – Lösungen: Herunterladen [pdf][280 KB]

Weiter zu Beweis 3