Weitere Übungen zu kgV und ggT

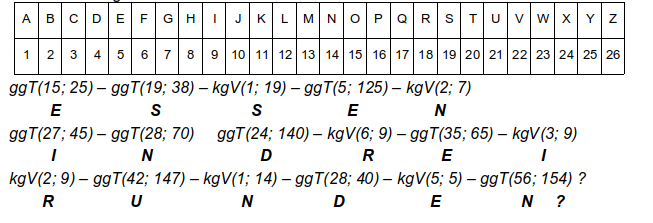
1. Während ihrer langweiligen Nachtschicht schickt Agentin Nü eine verschlüsselte Botschaft an Agent Mü. Entschlüssele sie.



2. Auf der Rasenfläche des Agenten-Hauptquartiers soll eine rechteckige Landefläche für Hubschrauber durch Lampen umrahmt werden. Die Landefläche soll 16 m lang und 12 m breit sein. Der Abstand der Lampen soll gleich groß sein und in „ganzen Metern“ gewählt werden. An allen vier Ecken muss eine Lampe gesetzt werden. Bestimme, wie viele Lampen dazu auf jeden Fall nötig sind.

   Der ggT(12; 16) beträgt 4. Der größtmögliche Abstand ist also 4 m. An jeder langen Seite sind damit 5 Lampen nötig, Mit diesen insgesamt 10 Lampen sind die Ecken bereits versorgt. An den beiden kurzen Seiten werden dann jeweils noch weitere 2 Lampen benötigt, insgesamt also 14 Lampen.

3. Aus vielen kleinen Bauklötzen mit den Maßen 3 cm x 5 cm x 6 cm soll ein Würfel gebaut werden. Berechne: Wie viele Bauklötze benötigt man dazu mindestens und welche Maße hat der Würfel dann?

   Hierzu wird das kgV aus drei Zahlen benötigt, da der Würfel in alle drei Dimensionen gleich lange Seiten haben muss. Das kgV(3; 5; 6) = 30. Somit hat der Würfel die Seitenlänge 30cm. Man benötigt nun 10 · 6 · 5 = 300 Bauklötze.

4. Beim sogenannten Cooper-Test darf man auf der 400m-Bahn im Leichtathletik-Stadion zwölf Minuten lang so viele Runden laufen, wie man schafft. Beim Sporttag der Agenten läuft Agent Mü gegen einen deutlich fitteren Kollegen. Während Mü für eine Runde 84 s benötigt, ist der Kollege bereits jeweils nach 72 s wieder an der Startlinie. Ermittle, ob es während des Cooper-Tests passiert, dass Mü die Startlinie gleichzeitig mit seinem Kollegen überquert.

   Nach dem Start würden sie erstmals wieder die Startlinie gleichzeitig passieren, wenn die Zeit dem kgV ihrer Rundenzeiten entspricht. Da das kgV(72; 84) = 504 beträgt, wäre es nach 504 Sekunden der Fall. Dies entspricht 8 Minuten und 24 Sekunden, ist also innerhalb der 12 Minuten eines Coopertests. Somit wird es passieren.

5. Der Keller des Agenten-Hauptquartiers wurde etwas niedriger gebaut als das Erdgeschoss. Vom Kellerboden zum Erdgeschossboden sind es 2,73 m. Vom Erdgeschossboden zum Boden des ersten Obergeschosses sind es dagegen 3,15 m. Dennoch verbindet eine Treppe den Keller mit dem ersten Obergeschoss, deren Stufen überall gleich hoch sind und in allen drei Geschossen mit dem jeweiligen Boden ohne Absatz abschließen. „Damit ist eigentlich klar, wie hoch die einzelnen Stufen sind!“, meint Agentin Nü. Erläutere, weshalb sie in ihrer Aussage den Ausdruck „eigentlich klar“ und nicht die Wortwahl „eindeutig klar“ verwendet.

   Die Treppenhöhe muss ein gemeinsamer Teiler von 273 cm und 315 cm sein, damit die Treppen ohne Versatz in allen Stockwerken enden.

   

6. * Überzeuge dich von der Richtigkeit der folgenden Aussage mithilfe einiger selbstgewählter Beispiele und begründe dann, dass sie allgemeingültig ist:

   „Das Produkt aus zwei Zahlen ist gleich dem Produkt ihres ggT mit ihrem kgV“

   Unten sind zwei Zahlen in ihre Primfaktoren zerlegt, die dann spaltenweise sortiert wurden. Man berechnet das kgV, indem man aus jeder Spalte einen Faktor auswählt. Dadurch hat man jede Spalte die nur einmal „besetzt“ ist komplett übernommen. Aus jeder vollständig besetzten Spalte hat man dagegen nur einen der beiden übereinanderstehenden Faktoren verwendet.

   Den ggT erhält man jedoch gerade als Produkt dieser füs kgV „nicht verwendeten“ Faktoren, da er aus jeder vollständig besetzten Spalte jeweils einen Faktor enthält.

   Somit ist das Produkt aus kgV und ggT gleich dem Produkt aus den beiden Zahlen.

   

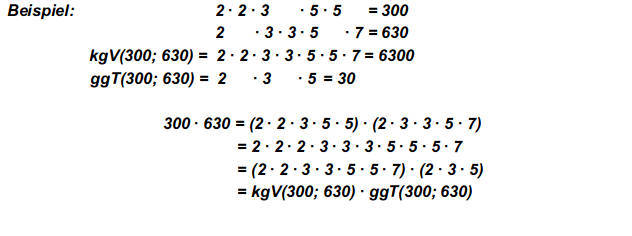
kgV und ggT – Lösungen: Herunterladen [odt][2 MB]

kgV und ggT – Lösungen: Herunterladen [pdf][463 KB]

Weiter zu Der Euklidische Algorithmus