Multigraphen – andere Reihenfolge
-
Königsberger Brückenproblem1
In der Innenstadt von Königsberg vereinen sich der Alte und der Neue Pregel zu einem Fluss, dem Pregel. Im 18. Jahrhundert führten sieben Brücken über die Flüsse. Folgendes Rätsel beschäftigte damals Königsberg und die mathematische Elite Europas:
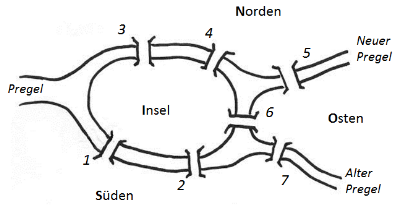
Kann man einen Stadtrundgang so planen, dass jede Brücke genau einmal überquert wird?
Diskutiert das Problem und sucht nach einer Lösungsstrategie.
Tipp: Mit Graphen lassen sich viele Probleme übersichtlich darstellen.
Das Nachtwächter-Problem
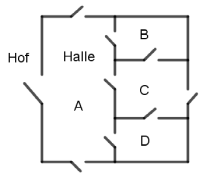
Ein Nachtwächter muss auf dem Betriebsgelände einer Firma mehrmals pro Nacht alle Türen eines Gebäudes mit 5 Hallen kontrollieren. Ist es möglich, dass er bei seinem Rundgang durch die Fabrikhallen jede Tür genau einmal passiert?
Multigraphen
Sind zwei Knoten durch mehrere Kanten verbunden, so spricht man von „Mehrfachkanten“ und nennt die zugehörigen Graphen Multigraphen. Ein Graph ohne Mehrfachkanten wird als „einfacher Graph“ bezeichnet.
-
Entfernt im Königsberger Stadtplan Brücken, so dass ein Stadtrundgang mit Rückkehr zum Ausgangspunkt möglich wird.
Ergänzt Brücken, anstatt welche zu entfernen, so dass dies gelingt.
-
Kann man einen Draht zu einem vollständigen Kantenmodell eines Würfels biegen? Zeichnet einen passenden Graphen und begründet damit eure Antwort.
Notiert, welche der folgenden Graphen Multigraphen sind. Begründet, ob es Eulersche Kantenzüge gibt und markiert ggf. Start.- und Endknoten.
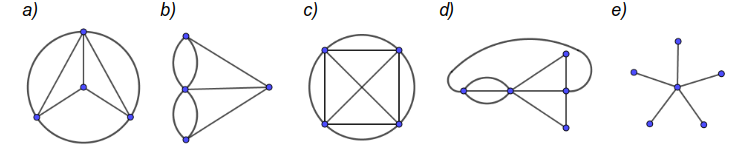
Fügt dem Graphen in 3e) möglichst wenige Kanten hinzu, so dass alle Knoten gerade sind.
1 Die erste Arbeit über Graphen (bzw. Graphentheorie) wurde von dem Schweizer Mathematiker Leonhard Euler (1701-1783) geschrieben. Sie erschien 1737 und begann mit dem berühmten Königsberger Brückenproblem.
Multigraphen – andere Reihenfolge: Herunterladen [odt][166 KB]
Multigraphen – andere Reihenfolge: Herunterladen [pdf][135 KB]
Weiter zu Hamiltonkreise
