Satz des Tha­les – Be­weis sei­nes Kehr­sat­zes

Stun­de 3

Der Satz des Tha­les wird nach den gän­gi­gen Lehr­wer­ken auf Basis des Bil­dungs­plans in Klas­se 7 ein­ge­führt und dabei von den Schü­le­rin­nen und Schü­lern auch ar­gu­men­ta­tiv be­grün­det. Seine An­wen­dung bei Kon­struk­ti­on von Tan­gen­ten oder der Be­rech­nung von Win­kel­wei­ten soll­te den Schü­le­rin­nen und Schü­lern eben­falls ver­traut sein.¹
Bei der Pla­nung der 3. Stun­de steht die Ent­schei­dung an, was man sei­ner Klas­se beim Be­weis des Kehr­sat­zes nun kon­kret zu­mu­ten kann und möch­te. Zur Ori­en­tie­rung fol­gen ver­schie­de­ne Va­ri­an­ten, wobei im Un­ter­richt die Kom­bi­na­ti­on von 2 bis max. 3 der nach­fol­gen­den Be­wei­se emp­foh­len wird, ggf. auch als Zu­satz­auf­trä­ge zur Dif­fe­ren­zie­rung. Be­mer­kun­gen zur Aus­wahl fol­gen dann im An­schluss an die Dar­stel­lung der Be­wei­se.

1) Be­weis mit Punkt­spie­ge­lung - Punkt­sym­me­trie des Recht­ecks

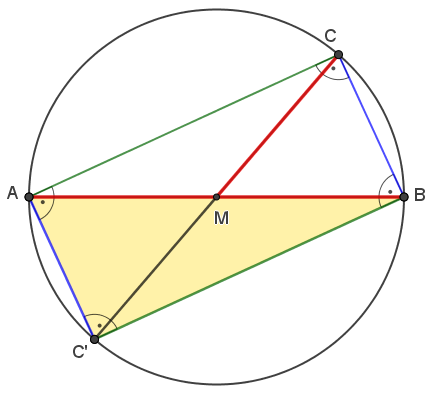
Vor.: Drei­eck ABC ist recht­wink­lig mit rech­tem Win­kel bei Punkt C.
Beh.: Punkt C liegt auf dem Kreis mit Durch­mes­ser AB.

Der Mit­tel­punkt M hal­biert die Stre­cke AB.
Die Punkt­spie­ge­lung an M bil­det das Drei­eck ABC auf das kon­gru­en­te Drei­eck A´B´C´ ab.
Da M Mit­tel­punkt von AB ist, gilt A´= B und B = A´.
Bei einer Punkt­spie­ge­lung ver­lau­fen Ge­ra­de und Bild­ge­ra­de par­al­lel: BC || AC´ und AC || BC´.
Sich ge­gen­über­lie­gen­de Sei­ten des Vier­ecks AC´BC sind also par­al­lel. Wegen des rech­ten Win­kels bei C , ist das Par­al­le­lo­gramm AC´BC au­ßer­dem ein Recht­eck.
In einem Recht­eck hal­bie­ren sich die Dia­go­na­len, es folgt MC=MA=MB.
C liegt daher auf dem Kreis um M mit Ra­di­us r=MC=MA=MB.

Ge­le­gent­lich be­geg­net man auch der ver­kürz­ten Ar­gu­men­ta­ti­on: „Durch Spie­ge­lung von C an M wird das Drei­eck ABC zu einem (punkt­sym­me­tri­schen) Recht­eck er­gänzt.“
Das wird allen SuS un­mit­tel­bar ein­sich­tig er­schei­nen, ist aber in der Ar­gu­men­ta­ti­on lü­cken­haft, da der Nach­weis fehlt, dass es sich tat­säch­lich um ein Recht­eck han­delt. Um den Un­ter­schied im Un­ter­richt zu ver­mit­teln, soll­te die Datei 00_­geo_tha­les_­um­keh­run­g_B1.ggb ge­nutzt wer­den. Die Ar­gu­men­ta­ti­on kann damit schritt­wei­se vi­sua­li­siert wer­den, ins­be­son­de­re wird die Punkt­spie­ge­lung dy­na­misch als Dre­hung dar­ge­stellt, so dass die ent­schei­den­de Par­al­lel­en­treue auch ein­sich­tig wird (diese ist den SuS i.d.R. ja nicht be­kannt).

2) Be­weis mit Um­kreis­mit­tel­punkt – Zen­tri­sche Stre­ckung

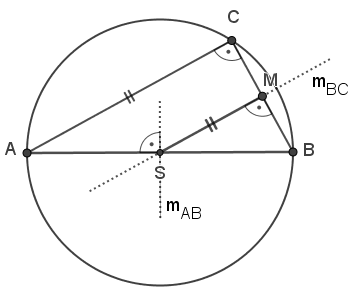
Vor.: Drei­eck ABC ist recht­wink­lig mit rech­tem Win­kel bei C.
Beh.: C liegt auf einem Kreis mit Durch­mes­ser AB.

Man be­trach­tet die Mit­tel­senk­rech­te m_BC durch den Mit­tel­punkt M der Seite BC. Sie schnei­de die Seite AB im Punkt S. Da ∠BMS=90° und ∠ CA=90° gilt, sind MS und CA par­al­lel und man kann den ers­ten Strah­len­satz an­wen­den: BS:BA=BM:BC=1:2, S hal­biert also die Seite AB.
Da S als Mit­tel­punkt der Seite AB auch auf deren Mit­tel­senk­rech­te m_AB liegt, ist S der Schnitt­punkt der Mit­tel­senk­rech­ten m_AB und m_BC. Nach dem Satz vom Um­kreis schnei­den sich die Mit­tel­senk­rech­ten im Mit­tel­punkt U des Um­krei­ses, es gilt daher S=U. C liegt als Eck­punkt auf die­sem Um­kreis.

3) Be­weis mit Um­kreis­mit­tel­punkt – Win­kel­sum­me in gleich­schenk­li­gen Drei­ecken

Vor.: (1) ABC sei ein Drei­eck mit den In­nen­win­keln α, β und γ, wobei γ=90° ist.

(2) M sei der Mit­tel­punkt der Stre­cke AB, dem Durch­mes­ser des Thal­e­s­krei­ses.

Beh.: C liegt auf einem Kreis um M.

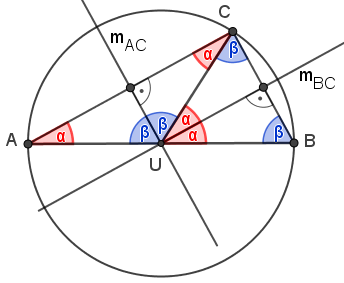
Man zeich­net die Mit­tel­senk­rech­ten m_BC und m_AC von BC und AC ein, ihr Schnitt­punkt ist der Um­kreis­mit­tel­punkt U, der auf m_AB liegt und daher gleich weit von A und B ent­fernt ist. Man zeigt, dass bei U ein ge­streck­ter Win­kel vor­liegt (∠AUB=180°), dass U=M gilt (bzw. dass U auf AB liegt).

Die Hilfs­stre­cke UC teilt den Win­kel bei C in die Teil­win­kel α und β. Man weiß, dass α+β=90° gilt, da bei C ein rech­ter Win­kel ge­ge­ben ist. Wegen der Sym­me­trie­ei­gen­schaf­ten der Mit­tel­senk­rech­ten sind die Drei­ecke AUC und UBC gleich­schenk­lig und es er­ge­ben sich auf­grund der Win­kel­sum­men die ein­ge­tra­ge­nen Win­kel­be­zie­hun­gen. Ins­be­son­de­re gilt ∠BUC=2α und ∠CUA=2β . Damit folgt: ∠AUB=∠BUC+∠CUA=2α+2β=2(α+β)=2*90°=180°, U liegt auf der Stre­cke AB und es gilt U=M.
Damit folgt MA=MC=MB=r, der Punkt C liegt auf dem Kreis um M mit Ra­di­us r.

Der letz­te Schritt be­ruht auf dem „Satz vom Um­kreis“. Falls man die­sen nicht ver­wen­den und von An­fang an nur die bei­den Mit­tel­senk­rech­ten be­trach­ten möch­te, kann hier mit der Sym­me­trie der Drei­ecke ar­gu­men­tiert wer­den, z.B.: „In den gleich­schenk­li­gen Drei­ecken gilt UA=UC (in Drei­eck USC) und UC=UB (in Drei­eck UBC), wor­aus u.a. UA=UB folgt, d.h. U hal­biert die Stre­cke AB und es gilt U=M.“

4) Be­weis durch Wi­der­spruch

Vor.: Das Drei­eck ABC be­sitzt im Punkt C einen rech­ten Win­kel.
Beh.: C liegt auf dem Thal­e­s­kreis mit Durch­mes­ser AB.

An­nah­me: Die Be­haup­tung sei falsch. C liege also nicht auf dem Thal­e­s­kreis über AB.
Man nimmt nun an, dass C ent­we­der in­ner­halb oder au­ßer­halb des Krei­ses liegt und führt je­weils einen Wi­der­spruch her­bei.

Vor­aus­set­zun­gen:

(1) ABC sei ein Drei­eck mit den In­nen­win­keln α, β und γ, wobei γ=90° ist.

(2) M sei der Mit­tel­punkt der Stre­cke AB, dem Durch­mes­ser des Thal­e­s­krei­ses.

An­nah­me 1:

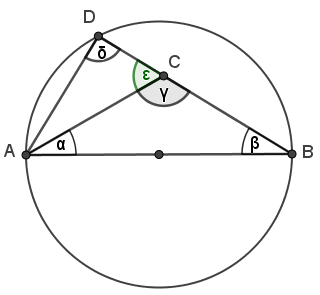
C liegt in­ner­halb des Thal­e­s­krei­ses.
Dann schnei­det die Ver­län­ge­rung der Stre­cke BC den Thal­e­s­kreis im Punkt D mit δ=∠ADB. Nach dem Satz des Tha­les folgt, dass δ=90°. Au­ßer­dem gilt γ+ε=180° (ge­streck­ter Win­kel bei C).
Da nach Vor­aus­set­zung γ =90° gilt, folgt damit auch ε=90°.

Das Drei­eck ACD be­sitzt somit zwei rech­te Win­kel und seine In­nen­win­kel­sum­me be­trägt mehr als 180°. Das er­gibt einen Wi­der­spruch zum In­nen­win­kel­sum­men­satz für Drei­ecke.
Die An­nah­me muss also falsch ge­we­sen sein,
C kann daher nicht in­ner­halb des Thal­e­s­krei­ses lie­gen.

An­nah­me 2:

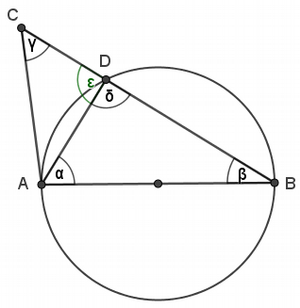
C liegt au­ßer­halb des Thal­e­s­krei­ses.
Dann schnei­det die Stre­cke BC den Thal­e­s­kreis im Punkt D mit . Nach dem Satz des Tha­les folgt, dass δ=90° . Au­ßer­dem gilt δ+ε=180°, also ist auch ε=90°. Da nach Vor­aus­set­zung γ=90° ist, be­sitzt das Drei­eck ADC zwei rech­te Win­kel und die Summe sei­ner In­nen­win­kel be­trägt somit mehr als 180°. Dar­aus er­gibt sich ein Wi­der­spruch zum Win­kel­sum­men­satz für Drei­ecke. Die zwei­te An­nah­me muss also eben­falls falsch ge­we­sen sein, C kann nicht au­ßer­halb des Thal­e­s­krei­ses lie­gen.

Damit ist be­wie­sen, dass der Punkt C unter den ge­ge­be­nen Vor­aus­set­zun­gen weder in­ner­halb noch au­ßer­halb des Thal­e­s­krei­ses lie­gen kann.
C muss daher auf dem Thal­e­s­kreis lie­gen.

5) Be­weis durch Kon­tra­po­si­ti­on

Für einen Satz A ⇒ B und seine Kon­tra­po­si­ti­on ¬B ⇒ ¬A gilt (A ⇒ B) ⇔ (¬B ⇒ ¬A).

Statt einen Satz zu be­wei­sen, kann man also auch des­sen Kon­tra­po­si­ti­on be­wei­sen, was mög­li­cher­wei­se ein­fa­cher ist.

Be­zo­gen auf den Kehr­satz des Sat­zes des Tha­les lau­ten die bei­den Aus­sa­gen:

Aus­sa­ge A: Drei­eck ABC hat bei C einen re­chen Win­kel.
Aus­sa­ge B: C liegt auf dem Kreis mit Durch­mes­ser AB.

Satz	A ⇒ B	Wenn das Drei­eck ABC bei C einen re­chen Win­kel be­sitzt, dann liegt C auf dem Kreis mit Durch­mes­ser AB.
Kon­tra­po­si­ti­on	¬B ⇒ ¬A	Wenn C nicht auf dem Kreis mit Durch­mes­ser AB liegt, dann gilt für den Win­kel γ beim Punkt C nicht γ=90°.

Da die Kon­tra­po­si­ti­on den Schü­le­rin­nen und Schü­lern in der Regel un­be­kannt sein dürf­te, soll­te sie zu­nächst sprach­lich be­tont wer­den wie in obi­gem Bei­spiel.

Kehr­satz des Sat­zes des Tha­les

Vor.: Drei­eck ABC hat bei C einen re­chen Win­kel.
Beh.: C liegt auf dem Kreis mit Durch­mes­ser AB.

Be­weis durch Kon­tra­po­si­ti­on:

Vor.: C liegt nicht auf dem Kreis mit Durch­mes­ser AB.
Beh.: Das Drei­eck ABC hat bei C einen Win­kel γ mit γ ≠ 90°.

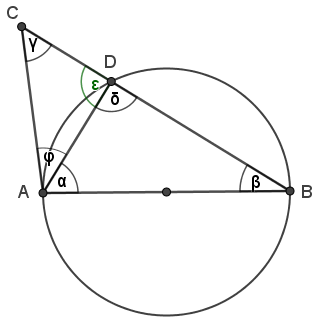
1. Fall:

C liegt au­ßer­halb des Krei­ses.
Dann schnei­det die Stre­cke BC den Thal­e­s­kreis im Punkt D mit δ=∠ADB. Nach dem Satz des Tha­les folgt, dass δ=90°. Au­ßer­dem gilt δ+ε=180°, also ist auch ε=90°.
Im Drei­eck ADC gilt daher wegen der Win­kel­sum­me
γ = 180°− (90°+φ) = 90° − φ < 90°
Für den 1. Fall gilt im Drei­eck ABC γ < 90°, also γ ≠ 90°.

2. Fall:

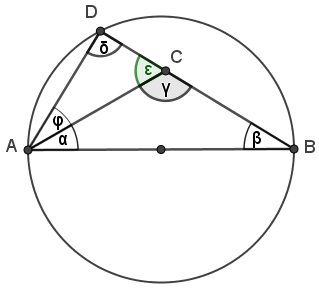
C liegt in­ner­halb des Krei­ses.
C liegt in­ner­halb des Thal­e­s­krei­ses.
Dann schnei­det die Ver­län­ge­rung der Stre­cke BC den Thal­e­s­kreis im Punkt D mit δ=∠ADB.
Nach dem Satz des Tha­les folgt, dass δ=90°.
Dann ist der Win­kel ε im Drei­eck ACD spitz, denn wegen der Win­kel­sum­me gilt ε = 90°− φ < 90°.
Dar­aus folgt, dass γ stumpf ist, denn γ ist Ne­ben­win­kel von ε und es gilt γ = 180°− ε > 90° (da ε < 90°).
Für den 2. Fall gilt im Drei­eck ABC γ > 90°, also γ ≠ 90°.

Ins­ge­samt ist damit be­wie­sen: „Wenn C nicht auf dem Thal­e­s­kreis über AB liegt, dann hat das Drei­eck ABC bei C kei­nen rech­ten Win­kel.“

Dar­aus folgt durch Kon­tra­po­si­ti­on: „Wenn das Drei­eck ABC bei C einen rech­ten Win­kel be­sitzt, dann liegt C auf dem Thal­e­s­kreis über AB.“

Be­mer­kun­gen zur Aus­wahl für den Un­ter­richt

Es wur­den 5 Va­ri­an­ten vor­ge­stellt, die ver­schie­de­ne As­pek­te ab­de­cken, an­de­re sind mög­lich. Die Be­wei­se 1 bis 3 wer­den di­rekt ge­führt und set­zen je­weils an­de­re in­halt­li­che Schwer­punk­te. Sie kön­nen in Ab­hän­gig­keit des vor­aus­ge­gan­ge­nen Un­ter­richts auch leicht va­ri­iert wer­den.

Der ab­bil­dungs­geo­me­tri­sche Be­weis 1 nutzt die Ei­gen­schaf­ten der Punkt­spie­ge­lung und die Punkt­sym­me­trie des Recht­ecks. Er kann bei Ein­satz des Geo­Ge­bra-App­lets gut als Ein­stieg ge­nutzt wer­den, um die Pro­ble­ma­tik her­aus­zu­ar­bei­ten und zu er­ken­nen, dass der Be­weis des Kehr­sat­zes eine sorg­fäl­ti­ge Ar­gu­men­ta­ti­on er­for­dert und schwie­ri­ger sein kann als der Be­weis des vor­aus­ge­hen­den Sat­zes.

Die Be­wei­se 2 und 3 gehen auf einem Spe­zi­al­fall des Sat­zes vom Um­kreis zu­rück: In einem recht­wink­li­gen Drei­eck liegt der Um­kreis­mit­tel­punkt auf der Hy­po­te­nu­se. Die­ser Zu­sam­men­hang muss al­ler­dings be­grün­det wer­den.

In Be­weis 2 wer­den mit­hil­fe des ers­ten Strah­len­sat­zes Sei­ten­ver­hält­nis­se über­tra­gen. Al­ter­na­tiv könn­te man hier auch eine ge­eig­ne­te zen­tri­sche Stre­ckung be­trach­ten. Be­weis 2 kann somit nur ein­ge­setzt wer­den, wenn die Ähn­lich­keit und Strah­len­sät­ze be­reits be­han­delt wur­den, wovon in der Regel aber aus­zu­ge­hen ist.
In Be­weis 3 er­fol­gen dazu Win­kel­be­trach­tun­gen unter Aus­nüt­zung von Sym­me­tri­en zur Mit­tel­senk­rech­ten, das soll­te pro­blem­los mög­lich sein.

Die Be­wei­se 4 und 5 sind aus di­dak­ti­scher Sicht in­ter­es­sant. Sie bie­ten den Vor­teil, dass die Lage von Punkt C dy­na­misch ge­se­hen und damit die Sicht aufs Ganze er­wei­tert wird. Es wer­den hier auch die Fälle ex­pli­zit be­trach­tet, bei denen C in­ner­halb oder au­ßer­halb des Krei­ses liegt. Da­durch wer­den Vor­stel­lun­gen an­ge­legt, die z.B. für die spä­te­re Ver­all­ge­mei­ne­rung des Sat­zes des Py­tha­go­ras zum Ko­si­nus­satz wich­tig sind.

Be­weis 4 bie­tet dar­über hin­aus die Ge­le­gen­heit, einen wei­te­ren Wi­der­spruchs­be­weis zu be­han­deln, nach­dem die­ses Be­wei­s­prin­zip in Klas­se 8 wahr­schein­lich ge­ra­de erst beim Be­weis der Ir­ra­tio­na­li­tät ein­ge­führt wurde.

Wenn die Um­keh­rung des Sat­zes des Tha­les in Schul­bü­chern be­han­delt wird, dann wird sie selt­sa­mer­wei­se meist durch Kon­tra­po­si­ti­on be­wie­sen.² Die­ses Be­wei­s­prin­zip ist den Schü­le­rin­nen und Schü­lern wegen den feh­len­den aus­sa­gen­lo­gi­schen Grund­la­gen aber fremd.
Be­weis 5 soll­te des­halb nur dann als Ver­tie­fung ge­wählt wer­den, wenn man in dem an­schau­li­chen und be­kann­ten Kon­text des Sat­zes des Tha­les tat­säch­lich das Prin­zip des „Be­wei­sens durch Kon­tra­po­si­ti­on“ ein­füh­ren möch­te. Es ver­langt SuS ei­ni­ges ab, könn­te aber in star­ken Lern­grup­pen durch­aus schon ein Ein­stieg in die For­ma­li­sie­rung der Aus­sa­gen­lo­gik sein, die dann ab Klas­se 9 auf dem Plan ste­hen wird.

 

---

 

Hin­ter­grund­in­for­ma­tio­nen: Her­un­ter­la­den [odt][432 KB]

Hin­ter­grund­in­for­ma­tio­nen: Her­un­ter­la­den [pdf][311 KB]

 

Wei­ter zu Win­kel­wei­ten be­stim­men