Teil­bar­keit und Teil­bar­keits­re­geln: Sum­men und Pro­duk­te

Quel­le: ZGP IMP

Die Teil­bar­keits­re­gel zum Tei­ler 6 ist ei­gent­lich keine ei­ge­ne Regel, son­dern nutzt aus, dass in der 6 die Tei­ler 2 und 3 „ver­steckt“ sind. Sol­che Ver­ste­cke we­cken na­tür­lich das In­ter­es­se un­se­rer Agen­ten. Lei­der sind aber nicht alle in die­ser Art ge­bil­de­ten Aus­sa­gen rich­tig. Kannst du ihnen hel­fen, die rich­ti­gen Aus­sa­gen her­aus­zu­fin­den?

Quel­le: ZPG IMP

1. a.) Agent Mü kennt eine schö­ne Prim­zahl: Die 102 356 789. Wenn man diese rück­wärts be­trach­tet, er­gibt sich eben­falls eine Prim­zahl, näm­lich 987 653 201. Sol­che Zah­len nennt man MIRP-Zah­len – wes­halb wohl¹? Aber Agent Mü hat ein ganz an­de­res Pro­blem: Er hat 102 356 789 mit 18 mul­ti­pli­ziert und das Er­geb­nis auf­ge­schrie­ben. Lei­der fehlt die letz­te Zif­fer auf sei­nem Blatt. Agen­tin Nü hat zwar kei­nen Ta­schen­rech­ner zur Hand, aber eine Idee: „Wir wis­sen doch, dass eine Zahl die durch 18 teil­bar ist, so­wohl durch 2, als auch durch 9 teil­bar ist. Damit ist die Sache doch klar.“ Was meint sie damit? Er­klä­re ihre Idee und führe sie durch, um die letz­te Zif­fer zu be­stim­men. Die Zahl lau­tet – bis auf die letz­te Zif­fer – 1 842 422 20_ .

   Teil­bar­keit durch 2

   (diese Über­le­gung ist zur Lö­sung letzt­lich un­nö­tig, geht aber se­kun­den­schnell):

   Die letz­te Zif­fer muss ge­ra­de sein, also fal­len die Zif­fern 1, 3, 5, 7 und 9 raus.

   Teil­bar­keit durch 9:

   Die Quer­sum­me muss durch 9 teil­bar sein, sie be­trägt 25 + x. Somit kann die End­zif­fer x nur die 2 sein.

   b.) Wie­der ist die letz­te Zif­fer ver­lo­ren ge­gan­gen. Die­ses Mal wurde 2³⁶ be­rech­net. Be­kannt ist nur noch: 2³⁶ = 6871947673x. Wel­che der Zif­fern 0 bis 9 kann x sein und wel­che nicht? Gib eine be­grün­de­te Aus­sa­ge über mög­lichst viele der zehn Mög­lich­kei­ten an.

   2³⁶ → Di­rekt er­sicht­lich ist: Die Zahl muss durch 2 teil­bar sein. Also kann x nur 0, 2, 4, 6 oder 8 sein.

   Die fol­gen­den bei­den wei­te­ren Lö­sungs­we­ge set­zen ein in­tui­ti­ves Ver­ständ­nis für die Po­tenz­re­chen­ge­set­ze vor­aus. Man kann aber auch durch die Schreib­wei­se aus der ge­schrie­be­nen Mul­ti­pli­ka­ti­on aus 36 Fak­to­ren „2“, die man in 18 „Zwei­er­grüpp­chen“ zu 18 Fak­to­ren „4“ bün­delt. Dies ist si­cher­lich nur in einer ge­führ­ten Ple­nums­pha­se fra­gend-ent­wi­ckelnd, oder von sehr leis­tungs­star­ken Schü­le­rin­nen und Schü­lern durch­führ­bar.

   2³⁶ = 4¹⁸ → Die Zahl muss durch 4 teil­bar sein. Also muss die aus den letz­ten bei­den Zif­fern ge­bil­de­te Zahl „3x“ durch 4 teil­bar sein. Somit kann es nur die Zif­fer 2 oder die 6 sein.

   2³⁶ = 4^{18 = 89}

   → Die Zahl muss durch 8 teil­bar sein. Also muss die aus den letz­ten drei Zif­fern ge­bil­de­te Zahl „73x“ durch 8 teil­bar sein Somit muss es die Zif­fer 6 sein.

   Al­ter­na­tiv kann man über die Zer­le­gung in Prim­fak­to­ren ar­gu­men­tie­ren:

   

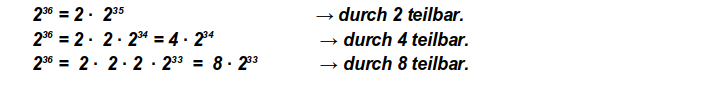
   c.)* Die Mul­ti­pli­ka­ti­on aller na­tür­li­chen Zah­len von einer Start­zahl n ab­stei­gend bis zur 1 nennt man Fa­kul­tät und kürzt sie mit n! ab (sprich:“ n Fa­kul­tät“). Zum Bei­spiel ist . Diese Zah­len wer­den schnell groß (z.B. 12! = 479 001 600). Ein WTR kann die Stel­len schon bald nicht mehr voll­stän­dig an­zei­gen² . Finde den­noch die feh­len­den Zif­fern x und y der fol­gen­den Glei­chung her­aus und er­klä­re dei­nen Lö­sungs­weg:

   35! = 10 333 147 966 386 1x4 929 666 651 337 523 200 000 y00

   Das Pro­dukt 35! be­steht aus 35 Fak­to­ren. Sechs davon be­inhal­ten den Fak­tor 5 ein­mal (5, 10, 15, 20, 30, 35), der Fak­tor 25 be­inhal­tet die 5 sogar zwei­mal. Somit ist der Fak­tor 5 acht­mal im Pro­dukt ent­hal­ten. Der Fak­tor 2 ist noch häu­fi­ger ent­hal­ten, so­dass aus den acht 5ern und acht der 2er genau acht 10er-Fak­to­ren ent­ste­hen. Somit muss die Zahl auf acht Nul­len enden, y ist also 0.

   Au­ßer­dem ist 35! durch alle Zah­len zwi­schen 1 und 35 teil­bar. Dar­un­ter ist auch die 9, deren Teil­bar­keits­re­gel sehr viel­ver­spre­chend ist, da die Quer­sum­me sel­ten Spiel­raum für zwei ver­schie­de­ne Zif­fern be­lässt. Die 11er-Regel ist im Kopf sogar noch ein­fa­cher lös­bar, da die al­ter­nie­ren­de Quer­sum­me klei­ner bleibt.

   Be­grün­dung mit 9er-Regel: Quer­sum­me ist 140 + x. Diese muss durch 9 teil­bar sein, dass ist nur der Fall, wenn x den Wert 4 an­nimmt.

   (wer ge­schick­ter vor­geht, ad­diert nicht alle Zif­fern , son­dern „igno­riert“ 9er und „9er-Päck­chen“)

   Be­grün­dung mit der 11er-Regel: Die al­ter­nie­ren­de Quer­sum­me be­trägt -4. Somit muss die feh­len­de Zif­fer 4 sein.