Hamiltonkreise – Übungen

Alle Hamilton-Kreise gesucht!

Findest du jeweils alle Hamilton-Kreise dieser Graphen? Zeichne sie in Dein Heft.
Europa per Bahn

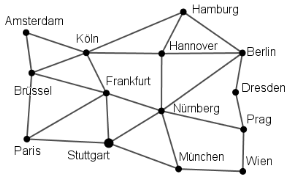
Svenja und ihre Freundin planen von Stuttgart aus eine Rundreise und möchten jede der Städte genau einmal besuchen. Untersuche, ob das möglich ist und zeichne ggf. einen Routenvorschlag ein.
Regelmäßige Fünfecke

Ein regelmäßiges Fünfeck kann als vollständiger Graph¹ mit fünf Knoten betrachtet werden. Es soll nun jeweils ein Kantenzug eingezeichnet werden, der genau einmal durch jeden Knoten geht und am Startpunkt endet. Dabei sind vier verschiedene geometrische Formen möglich. Zeichne sie unten ein. Probiere aus und zeichne bei Bedarf weitere Versuche ins Heft.

Zusatz: Wie viele verschiedene Hamiltonkreise gibt es in einem „Vollständigen Fünfeck“?
LKW-Tour

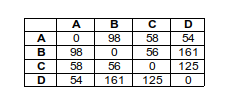
Herr Schnell muss Waren ausliefern. Er startet bei seiner Spedition in A, muss dann jede der Städte B,C und D genau einmal anfahren und wieder zur Spedition in A zurückkehren. Die Entfernungen sind in der Tabelle (in km) angegeben.

a) Er möchte auf seiner Tour jeweils in die nächst-gelegene noch nicht besuchte Stadt fahren und am Ende nach A zurückkehren. Wie lang ist sein Weg?

b) Zeichne einen bewerteten Graphen. Suche alle Hamiltonkreise und ermittle die kürzeste Route.
Hamiltons Spielbrett²

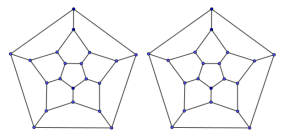
Dieser Graph mit 20 Knoten entsteht, wenn man das Bild eines Dodekaeders (12-Flächner) in der Zeichenebene so darstellt, dass sich seine Kanten nicht überschneiden. Er heißt deshalb auch Dodekaedergraph. Zeichne 2 verschiedende Hamiltonkreise ein.

¹ Ein Graph heißt vollständig, wenn jeder Knoten mit jedem anderen Knoten durch genau eine Kante verbunden ist. Der Graph in Aufgabe 3 wird übrigens auch als „Vollständiges Fünfeck“ bezeichnet.

² William R. Hamilton hat auch ein Spiel erfunden, bei dem er einen Dodekaedergraphen als Spielbrett nutzte.

Hamiltonkreise – Übungen: Herunterladen [odt][159 KB]

Hamiltonkreise – Übungen: Herunterladen [pdf][143 KB]

Weiter zu Graphen als Tabellen