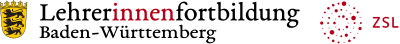Graphen
1. Stunde: Eulersche Kantenzüge
| Ablauf und Inhalte | Hinweise |
|
|
Erläuterungen
Der nicht zusammenhängende Multigraph mit Schlinge am rechten Rand hat 9 Knoten und 10 Kanten. Er bietet Gelegenheit zur Präzisierung der Definition. Lassen Sie z.B. Kanten und Knoten zählen bzw. beschreiben. Dabei lassen sich u.a. folgende Aspekte thematisieren:
- isolierte Knoten („Augen“) als Knoten ohne Kanten („mit der Ordnung 0“), daraus resultierende Aufteilung in drei Teilgraphen, die nicht zusammenhängen,
- Schlinge (am Kopf) als Kante, die einen Knoten mit sich selbst verbindet,
- doppelte Kanten unten als Mehrfachkanten (bzw. Multikanten),
- die topologisch nicht relevante „Überlagerung“ von Kanten
und möglicherweise auch das zentrale Merkmal eines Graphen als topologische Struktur: Die „Verformbarkeit“, ohne dabei seine wesentlichen Eigenschaften zu verlieren. Die Invarianz gegenüber Verformungen lässt sich dabei dynamisch gut mit der Datei 01_aug_ab_graph_drachen.ggb visualisieren, indem man an geeigneten Punkten „zieht“.
Eine systematische Ergebnissicherung ist an dieser Stelle nicht sinnvoll, gleichwohl können Schwerpunkte gesetzt und ausgewählte Aspekte an der Tafel festgehalten werden.
Kommentare zu den einzelnen Aufgaben bzw. Aufträgen:
Zusammenhängende Graphen
Die Aufgabe bietet einen ersten „weichen“ Einstieg und soll das Verständnis für die besonderen Eigenschaften zusammenhängender Graphen entwickeln, da die notwendigen und hinreichenden Bedingungen für die Existenz Eulerscher Kantenzüge nur für diese Graphen gelten.
Eulersche Kantenzüge (EKZ)
Die Aufgabe eröffnet zunächst einen enaktiven Zugang über das mentale Suchen bzw. das aktive Nachzeichnen verschiedener Eulerscher Kantenzüge, erste Gesetzmäßigkeiten werden möglicherweise entdeckt und bei den Präsentationen ausgetauscht.
Erarbeitung der allgemeinen Regel (hinreichende Bedingung für EKZ)
Falls Sie die Definition der Ordnung eines Knotens hier nicht angeben und statt dessen flexibel im Erarbeitungsprozess einbringen bzw. danach ergänzen möchten, löschen Sie sie bitte auf dem Arbeitsblatt.
Zur Unterstützung bietet sich bei Bedarf der Zusatzauftrag an, geeignete Start- und Endknoten zu markieren (siehe Lösung). Einige Schülerinnen und Schüler werden aber auch ohne diese Hilfe auf die richtige Idee kommen, allerdings wird die Formulierung der Vermutung sicherlich eine Herausforderung bleiben.
Optionales „Rollenspiel“ zur inhaltlichen Vorbereitung
5 S. stellen sich als „Haus des Nikolaus“ auf, sie „spielen“ die Knoten, die Kanten bleiben zunächst unsichtbar. Ein S. spannt zwischen den „Knoten“ mit einem Wollfaden „seinen“ Eulerschen Kantenzug auf. Jedes Mal, wenn er dabei einen Knoten passiert, nennt der Mitschüler die Ordnung „seines“ Knotens, die Anzahl der ankommenden und weggehenden Kanten. Hier muss einmalig geklärt werden, dass der durchgehende Wollfaden als 2 Kanten gezählt werden muss. Durch die didaktische Umkehrung des Problems wird so ein Graph generiert, der einen Eulerschen Kantenzug enthält und die hinreichende Bedingung („höchstens zwei ungerade Knoten“) wird intuitiv erfahrbar. Durch das Hochzählen der Knotenordnungen wird die Formulierung einer allgemeinen Regel vorbereitet. Es wird die Einsicht angebahnt, dass sich die Ordnung beim Durchlaufen eines Knotens immer um 2 erhöht. Alternativ könnte statt einem Rollenspiel auch ein enaktiver Zugang in Partnerarbeit angeboten werden, bei dem jedes Team mit einem Wollfaden (genau passender Länge) einen EKZ in einem Modell eines Graphen spannen muss (z.B. Holzbrett mit Nägeln oder Korkplatte mit Stecknadeln o.ä.). Hierbei wären alle SuS aktiv eingebunden.
Formulierung einer allgemeinen Regel
Einen Vorschlag finden Sie in der Musterlösung, es sind aber viele Varianten sind denkbar. Formulierungen der SuS werden meist auf Bewegungsvorstellungen basieren und müssen ggf. noch ergänzt werden, z.B. könnte formuliert werden:
- „Knoten, in die gleich viele Kanten hinein- wie hinausführen“ …
- „man verlässt einen Knoten genau so oft wie man bei ihm ankommt ...“
Mögliche Formulierungsvariante nach dem Rollenspiel:
„Beim Durchlaufen eines Knotens erhöht sich seine Ordnung immer um 2, da jeweils eine hin- und eine wegführende Kante zu zählen sind. Beim Start- und Endknoten erhöht sich die Ordnung nur um „1“, so dass sie ungerade bleibt. Nur wenn man zum Ausgangspunkt zurückkehrt, hat auch der Start-Endknoten eine gerade Ordnung.“
Zur Orientierung hier noch zwei Schülerformulierungen aus der Erprobung:
„Bei mehr als zwei ungeraden Knoten gibt es keinen EKZ. Wenn von zwei Knoten eine ungerade Anzahl von Kanten ausgeht und von allen anderen Knoten eine gerade Anzahl, so gibt es einen EKZ, der offen ist. Wenn es nur Knoten mit gerader Kantenanzahl gibt, so gibt es einen EKZ, der geschlossen ist. “
„Wenn die Ordnungen aller Knoten gerade ist, so gibt es einen geschlossenen EKZ. Wenn ein Graph ungerade Knoten enthält, so gibt es nur dann einen EKZ, wenn es genau zwei ungerade Knoten sind, ein Start- und ein Zielknoten.“
Reflexion am Stundenende
Eulersche Kantenzüge sind wie bereits erwähnt nur in zusammenhängenden Graphen möglich, was aber an dieser Stelle nicht im Fokus steht und deshalb leicht vergessen wird. Man könnte dies abschließend hinterfragen, eventuell auch mit einem der folgenden Gegenbeispiele an der Tafel problematisieren:

Lassen sich Knoten ergänzen, so dass im neuen zusammenhängenden Graphen ein EKZ existiert? Lassen sich Brücken hinzufügen, so dass ein EKZ möglich ist? Welche Möglichkeiten gibt es?
Vertiefungsmöglichkeiten:
Präzise Formulierungen wie „Es darf höchstens 2 ungerade Knoten geben“ sind nicht zu erwarten, könnten aber gemeinsam wie oben skizziert entwickelt werden, wenn man zuvor erarbeitet, dass es keinen Graphen mit nur einem ungeraden Knoten geben kann.
Reflexionsanregende Fragen:
Warum ist die Summe der Ordnungen aller Knoten das Doppelte der Kantenzahl? Warum ist die Anzahl der Knoten mit ungerader Ordnung immer gerade?1 Gilt dies nur in zusammenhängenden Graphen? …
Hinweis: Das Rollenspiel bietet sich auch an, wenn man solche Fragen zur Vertiefung stellen möchte. Dann könnte man mit dem Wollfaden auch einen „beliebigen“ Multigraphen mit EKZ erzeugen, der dann als Graph mit Mehrfachkanten an die Tafel übertragen wird, um ausgehend vom konkreten Beispiel Antworten zu finden.
Abschließender Warnhinweis zu kombinatorischen Nebenschauplätzen
Auf die Frage nach der Anzahl der möglichen EKZ sollte man vorbereitet sein und wissen wie gefährlich sie im Unterricht werden kann. Sie eröffnet je nach Graph ungeahnte kombinatorische Welten, die an dieser Stelle auf jeden Fall gemieden werden sollten. Bei 2a) („Haus des Nikolaus“) wären es z.B. schon 44·2=88 verschiedene Eulersche Kantenzüge. Die Anzahl ist nicht ohne Weiteres erkennbar, man braucht Geduld und Zeit.
Bei 2d) wären es immer noch 16·2=32 Varianten. Solche kombinatorischen Aspekte bieten Potenzial für binnendifferenzierende Zusatzaufträge, die dann aber auch angemessen nachbereitet werden müssen und Zeit erfordern. Bei 2b) hängt die Anzahl z.B. von der Wahl des Startknotens ab, insgesamt ergeben sich hier 8·2·3·2+2·4·3·2=144 verschiedene EKZ.
1 Gedankengang zum Nachweis z.B. in: „Schülerduden Die Mathematik I“, Dudenverlag, 1990, 5. Auflage, S.164 oder in: Peter Tittman: „Graphentheorie- eine anwendungsorientierte Einführung“, Hanser, 2011, 2. Auflage, S.14
2. Stunde: Multigraphen – Königsberger Brückenproblem
| Ablauf und Inhalte | Hinweise |
|
|
Erläuterungen
In der Titelzeile wurde als Logo ein Multigraph eingebunden: Das „Haus des Nikolaus mit Keller“. Falls Ihnen der Einstieg im Kontext des Königsberger Brückenproblems für Ihre Klasse schwierig erscheint, könnten Sie auch diesen Graphen zur Einführung von Multigraphen verwenden: Was müsste man am „Haus des Nikolaus“ ändern, damit man beim Zeichnen in einem Zug am Ausgangspunkt endet? Ein geschlossener Eulerscher Kantenzug wird möglich, wenn zwischen beiden ungeraden Knoten eine Kante hinzugefügt wird, man erhält den Keller ...
Königsberger Brückenproblem
Das Problem des Stadtrundgangs wird auf auf das Zeichnen eines Graphen in einem Zug zurückgeführt (Strategie des Zurückführens auf bekannte Zusammenhänge). Die Erarbeitung sollte dabei auf die Klasse abgestimmt werden:
- Löschen Sie den Tipp, wenn Sie die Aufgabe offener stellen möchten.
- Geben Sie weitere Tipps im Laufe der Erarbeitung, falls Sie Probleme erwarten, z.B.
„Zeichnet einen möglichen Graphen ein / fasst Brücken als Kanten auf“, oder „Sucht nach Eulerschen Kantenzügen / notiert neben den Knoten ihre Ordnung“.
In Aufgabe 3b) ist bereits ein Graph eingebunden, der genutzt werden könnte.
Aufgabe 2 ist zur Wiederholung der Begrifflichkeiten und zur Übung gedacht.
Der binnendifferenzierende Zusatzauftrag kann durch Verwendung der eingeführten Begriffe anders formuliert werden, z.B. „Fügt dem Graph möglichst wenige Kanten hinzu, so dass ein geschlossener Eulerscher Kantenzug existiert“.
Nachtwächter-Problem
Hier kann man bei Bedarf den Tipp geben, dass der Hof als Gebiet berücksichtigt werden muss. Die Aufgabe kann übersprungen oder als Hausaufgabe gegeben werden, falls zu wenig Zeit vorhanden sein sollte.
Optionale Vertiefung des Königsberger Brückenproblems
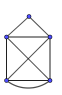
Alle Knoten haben ungerade Ordnung, entfernt man eine Kante (bzw. Brücke), so haben danach zwei der vier Knoten eine gerade Ordnung. Dann ist ein offener Eulerscher Kantenzug möglich, aber die geforderte Rückkehr zum Ausgangspunkt bleibt unmöglich. Mann muss daher mindestens 2 Brücken entfernen. Damit alle Knoten gerade Ordnung haben, muss eine der Brücken 1,2,3,4 und die richtige der Brücken 5 oder 7 entfernt werden.
Tatsächlich wurde in Königsberg eine 8. Brücke über den Pregel und eine 9. Brücke über den Alten Pregel gebaut2 , so dass heute „Euler-Spaziergänge“ (Eulerwege) über alle Brücken möglich sind, allerdings kann man nach wie vor nicht zum Ausgangspunkt zurückkehren.
Aufgabe 5 ist zur Differenzierung gedacht und bindet die dritte Dimension ein.
In stärkeren Lerngruppen bietet sich hier ein kurzer Exkurs zu „planaren bzw. plättbaren Graphen“ an, bei denen Überschneidungen von Kanten in der ebenen Darstellung nicht erlaubt sind.3
2 Eintrag „Netz“, in: „Schülerduden Die Mathematik I“, Dudenverlag, 1990, 5. Auflage, S.311, 312
3 Vgl. dazu Kap 8: „Vom Körper zum Graphen“, in Nitzsche: „Graphen für Einsteiger“, Vieweg+Teubner, Wiesbaden, 2009, 3. Auflage, S.5, S.165 ff. Insbesondere die 5 „Platonischen Graphen“ (S.179) wären reizvolle Objekte.
3. Stunde: Hamilton-Kreise – „Travelling-Salesman-Problem (TSP)“
| Ablauf und Inhalte | Hinweise |
|
|
Erläuterungen
Im Bildungsplan ist der Fachbegriff Hamiltonscher Kantenzug ausgewiesen. In der Literatur ist dagegen die Bezeichnung Hamilton-Kreis üblich, der daher hier eingebunden und bevorzugt verwendet wurde. Es wurde darauf verzichtet, im Kontext Hamiltonscher Graphen auch offene Kantenzüge zu betrachten.
Da wenig Zeit zur Verfügung steht und mit den Begriffen nicht angemessen weiter gearbeitet werden kann, wurden folgende möglichen Definitionen noch nicht eingebunden:

Da es sich um zentrale Begriffe der Graphenthoerie handelt, ist es eine Überlegung wert, diese in stärkeren Lerngruppen einzuführen und eulersche von hamiltonschen Graphen abzugrenzen. Dazu bietet sich beispielsweise folgende Aufgabe an4 :
Welche der Graphen sind eulersch, welche hamiltonsch?
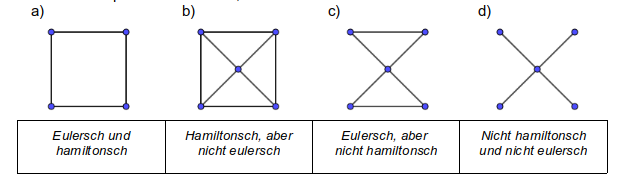
„Hamiltonsch und eulersch … sind zwei auf den ersten Blick ähnliche, aber ganz verschiedene Eigenschaften. Natürlich kann man auch bei einem hamiltonschen Graphen eine Kante nicht doppelt durchlaufen, weil man ja sonst durch die End-Ecken dieser Kante zweimal käme.“5
Hinweise zu den einzelnen Aufgaben:
Hamilton-Kreise
Ausgehend von der Definition geht es in Aufgabe 1 zunächst um eine rein geometrische Annäherung an Hamiltonsche Kantenzüge. Im b)- und d)-Teil wurden zur Präzisierung Graphen gewählt, in denen Kantenzüge existieren, die jeden Knoten enthalten, aber nicht geschlossen sind. Dies kann bei der Auswertung des binnendifferenziert angelegten Zusatzauftrages thematisiert werden.
Bewertete Graphen
Zur Einführung wurde als Kontext eine einfache Städtetour gewählt und der bewertete Graph vorgegeben6, um zügig zur Behandlung eines ersten einfachen TSP zu gelangen.
„TSP“ - Travelling-Salesman-Problem
Auch hier wurde ein einfaches TSP mit nur 4 Städten gewählt, um den Fokus im Unterricht nicht auf kombinatorische Überlegungen zu setzen. Folgender Hinweis könnte für Schülerinnen und Schüler in der Reflexionsphase interessant sein: Im Gegensatz zu den leichter zugänglichen Eulergraphen machen Hamiltongraphen den Mathematikern das Leben noch ziemlich schwer. Es wurde noch kein einfacher Algorithmus gefunden, mit dem man entscheiden kann, ob ein Hamiltongraph vorliegt. In der Praxis interessiert vor allem in bewerteten Graphen das Auffinden des Hamiltonskreises mit niedrigstem Wert mit vertretbarem Rechenaufwand. Eine Methode ist noch nicht bekannt, obwohl viele Mathematiker mit Hochdruck in diesen Bereichen forschen. Das „TSP" ist momentan noch nicht gelöst, es bleibt ein vielleicht unlösbares Problem. Die enorme Menge an zu vergleichenden Hamiltonkreisen macht dies einsichtig: Wenn in einem vollständigen Graphen mit n Knoten jeder Knoten mit jedem anderen durch eine Kante verbunden ist, so existieren
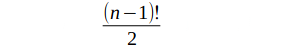
Hamiltonkreise.
Bei unserem Einstiegsbeispiel waren es 3 Routen (bzw. Hamiltonkreise), die noch gut ausgewertet werden können. Bei 5 Städten sind es 12, bei 6 Städten 60 Hamiltonkreise. Bei 20 Städten wären es unglaubliche 1 216 451 004 088 320 000 Hamiltonkreise ...7
Isomorphe Graphen
Diese Aufgabe kann als vertiefende Übung von allen Schülerinnen und Schülern bearbeitet werden. Sie dient als Puffer, gibt aber im Sinne der Differenzierung auf dem Lösungsblatt einen Ausblick auf die „topologische Äquivalenz“ von Graphen. Weitere kleine Aufträge zum „Umzeichnen“ der Hamiltongraphen auf dem Arbeitsblatt könnten sich anschließen.
Auch der Rückbezug zum „Haus des Nikolaus“ könnte im Unterricht aufgegriffen werden, indem Verformungsschritte diskutiert und visualisiert werden:
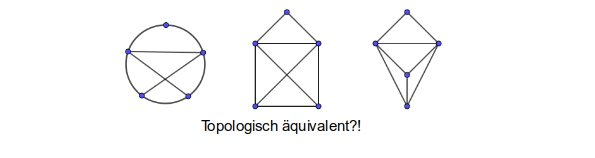
So könnte sich auch der „Kreis“ dieser kurzen Einführung in die Graphentheorie an dieser Stelle schließen.
Für die anschließende 4. Stunde der Einheit wird die optionale Behandlung von Adjazenzmatrizen empfohlen, die in altersangemesser Form als Nachbarschaftstabellen eingeführt werden. Durch die numerisch basierte Darstellung verschiedener Graphen erfolgt dabei ein Perspektivwechsel, der ein vertieftes Verständis der Eigenschaften von Graphen ermöglicht und dadurch den reflektierten Umgang mit Datenstrukturen im Bereich der Informatik unterstützt.
4 Quelle: Nitzsche: „Graphen für Einsteiger“, Vieweg+Teubner, Wiesbaden, 2009, 3. Auflage, S.40
5 a.a.O., statt „End-Ecken“ wird der Begriff Endknoten empfohlen.
6 In Anlehnung an das Beispiel im Abschitt „Eine billige Rundreise“, in Nitzsche: „Graphen für Einsteiger“, Vieweg+Teubner, Wiesbaden, 2009, 3. Auflage, S.52
7 A.a.O., S.53
4. Stunde: Graphen als Tabellen – Isomorphie von Graphen
| Ablauf und Inhalte | Hinweise |
|
|
Erläuterungen
Nachbarschaftstabellen und isomorphe Graphen
Vordergründig geht es zunächst nur darum, das Konzept der Nachbarschaftstabellen zu verstehen und an 5 Beispielen anzuwenden. Gleichzeitig wird die Aufgabe aber auch zur Erarbeitung von Vorstellungen zur Isomorphie genutzt. Für die schnelleren SuS sind dazu Entdeckungen möglich, die über den differenzierenden Zusatzauftrag angeregt werden.
Hinführung zu einer altersgerechten Definition zur Isomorphie von Graphen
Nach den Präsentationen der 5 Tabellen schließt sich eine Weiterführungsphase zur Definition des Begriffs isomorph an. Geben Sie den Entdeckungen der SuS hier Raum, wahrscheinlich werden sie eigenständig auf die Invarianz zentraler Eigenschaften bei Verformung kommen. Die Datei 04_aug_ab_isomorphe_graphen.ggb bietet die Möglichkeit, die Verformung der Graphen von Aufgabe 1 dynamisch zu visualisieren. Sie sollte erst in der Zusammenführungsphase eingesetzt werden, nachdem die SuS ihre Sichtweisen und Ideen entwickeln konnten. Zur Weiterführung wird abschließend eine Definition an der Tafel festgehalten, hier ein altersangemessen reduziertes Beispiel: Alle für Graphen typischen Eigenschaften wie Anzahl der Knoten, Anzahl der Kanten und Ordnungen der Knoten müssen bei gleicher Nachbarschaftsstruktur übereinstimmen.
Dazu kann man ggf. die Knoten eines der beiden Graphen umnummerieren bzw. umbenennen. Der Aspekt der Umnummerierung kann, falls die SuS es noch nicht angesprochen haben, durch die Gegenüberstellung der Graphen d) und e) (bzw. c) und e)) erarbeitet werden.
Die beiden Graphen in c) und d) sind isomorph zueinander. Nur wenn die Bezeichnungen („label“) keine Rolle spielen, sind sie auch isomorph zum Graphen in e). Als gelabelte Graphen sind sie nicht isomorph, da ihr „Nachbarschaftsgefüge“ nicht übereinstimmt.
Zur Abrundung könnte man für Graph e) nach der gemeinsamen Umbenennung der Knoten (Vertauschen der Namen von A und D) erneut eine Tabelle erstellen lassen, die dann identisch zu den Nachbarschaftstabellen von c) und d) wäre.

Zur Isomorphie von Graphen könnte man zuvor altersangemessen festhalten: Die Datei 04_aug_animierte_Umformung_Haus_des_Nikolaus.ggb kann ergänzend oder alternativ eingesetzt werden, um die Isomorphie zweier Graphen ausgehend vom bekannten „Haus des Nikolaus“ zu visualisieren.8
Vertiefung der Definition
Zur Untersuchung auf Isomorphie betrachtet man sogenannte Grapheninvarianten. Sobald eine zentrale Eigenschaft nicht übereinstimmt, können zwei Graphen nicht isomorph sein. Im a), b) und c) -Teil reicht es aus, die offensichtlichen Eigenschaften Knoten- bzw. Kantenanzahl und Knotenordnungen zu überprüfen. Im d) Teil reicht dies nicht, hier muss das Strukturgefüge (der Zusammenhang zwischen den Komponenten) untersucht werden.
Graphen zu vorgegebener Tabelle zeichnen
Die Umkehrung der Aufgabenstellung in Aufgabe 3 liefert aus didaktischer Sicht den schönen Nebeneffekt, dass die topologische Äquivalenz von Graphen und die zentrale Bedeutung der Matrizen (bzw. in Klasse 8 Tabellen) während der Bearbeitung intuitiv erfasst werden können. Durch den Darstellungswechsel zwischen Bild und Tabelle wird außerdem ein vertieftes Verständnis der bereits eingeführten Begriffe erreicht. Ein weiteres Beispiel hierzu findet sich bei den vertiefenden Übungsaufgaben (Nr. 2).
Reflexion – weitere Anknüpfungspunkte
Passende Fragen wurden auf diesem Arbeitsblatt bereits eingebunden, sollten aber für die Lerngruppe modifiziert werden. Andere Aspekte könnten ebenso in den Blick genommen und vertieft werden, z.B.:
Woran erkennt man einen isolierten Knoten?
Warum ist diese Tabelle symmetrisch zu einer ihrer Diagonalen?
Was verändert sich, wenn man zwei Knotennamen vertauscht?
Wie viele und welche Einträge müssten dann genau getauscht werden?
Wie sieht die Nachbarschaftstabelle eines vollständigen Graphen aus?
8 Vgl. Erläuterungen zur Isomorphie von Graphen in der Datei 01_aug_hintergrund.odt auf Seite 6.
Unterrichtsverlauf: Herunterladen [odt][407 KB]
Unterrichtsverlauf: Herunterladen [pdf][435 KB]
Weiter zu Aussagenlogik