Das kleinste gemeinsame Vielfache – kgV

Wenn Agent Mü 12 Minuten für einen Rundgang benötigt und Agentin Nü 28 Minuten, dann treffen sie erstmals nach 84 Minuten wieder im Wachraum aufeinander. Agent Mü hat dann sieben Runden „gedreht“, während Nü dreimal unterwegs war. Mathematisch betrachtet ist die Zahl 84 das Siebenfache von 12 und das Dreifache von 28. Sie ist somit ein Vielfaches von 12 und ein Vielfaches von 28. Eine solche Zahl nennt man gemeinsames Vielfaches von 12 und 28. Auf der Suche nach weiteren gemeinsamen Vielfachen von 12 und 28 findet man beispielsweise die Zahlen 168 und 252. Man findet jedoch keine kleinere Zahl als 84 als gemeinsames Vielfaches von 12 und 28. Deshalb nennt man die Zahl 84 das kleinste gemeinsame Vielfache von 12 und 28, kurz das kgV(12; 28). Das kleinste gemeinsame Vielfache darf dabei auch die größere der beiden Zahlen sein, so ist zum Beispiel kgV(12; 24) = 24.

Aufträge:

1. Bestimme die folgenden kleinsten gemeinsamen Vielfachen:

   a.) kgV(6; 7)

   b.) kgV(12; 18)

   c.) kgV(14; 18)

   d.) kgV(84; 102)

2. Die Primfaktorzerlegungen mehrerer Zahlen lassen sich geschickt vergleichen, wenn man gleiche Primfaktoren untereinander schreibt, z.B. für die Zahlen 300 und 630 so:

   

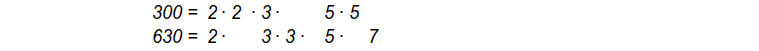
   a.) Führe dies für die Zahlen aus Aufgabe 1 durch. Schreibe dazu für jede Teilaufgabe die Primfaktorzerlegungen der beiden Zahlen und des kgV in drei Zeilen untereinander. Überlege dir eine Regel, wie man aus den Primfaktorzerlegungen der beiden Zahlen auf deren kgV kommen kann, und schreibe sie auf.

   b.) Überprüfe deine Regel an weiteren Zahlenpaaren und deren kgV.

   c.) Bestimme das kgV(9000; 41580) mit

   9000 = 2 · 2 · 2 · 3 · 3 · 5 · 5 · 5 und

   41580 = 2 · 2 · 3 · 3 · 3 · 5 · 7 · 11

3. Agent Mü muss mal wieder einen Tresor knacken. Dazumuss er eine Zahl auf einem Ziffernfeld eingeben. DieEingabezahl lässt ein kleines Zahlenrad genau so oft um sichselbst drehen. Der Tresor geht auf, wenn sich dadurch dasgroße Zahlenrad wieder an der gleichen Position wie vor derEingabe befindet. Was muss er eingeben?

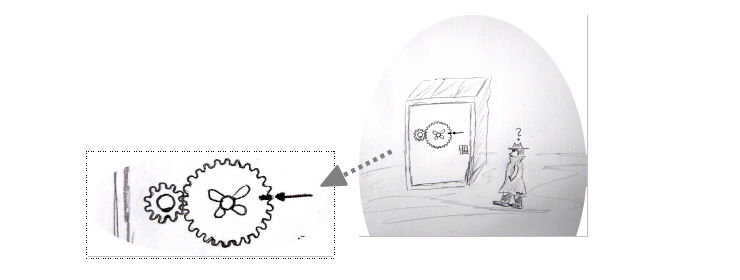
Quelle: ZPG IMP

1. * „Das kgV kann bei der Addition und Subtraktion von Brüchen sehr hilfreich sein.“

   Wie ist diese Aussage gemeint? Führe zunächst einige Beispieladditionen von Brüchen durch. Überlege dabei: Wie kann das kgV welcher Zahlen geschickt eingesetzt werden? Wie kann / würde man ohne die Kenntnis dieses kgV vorgehen? Formuliere dann eine Vorgehensweise zur Addition und Subtraktion von Brüchen, in der das kgV (geschickt) eingesetzt wird.

kgV und ggT: Herunterladen [odt][2 MB]

kgV und ggT: Herunterladen [pdf][435 KB]

Weiter zu ggT