Ein modernes Verschlüsselungsverfahren: AES
Material:
-
CrypTool 11
Das AES-Verfahren (Advanced Encryption Standard ) ist ein aktuell verwendetes symmetrisches Verfahren. Auch: Rijndael-Verfahren oder Rijndael-Algorithmus.
Es wurde von Joan Daemen und Vincent Rijmen entwickelt und im Jahr 2000 vom National Institute of Standards and Technology (NIST) als Standard festgelegt. Es wurde notwendig, weil durch höhere Rechnerleistung bisherige Verschlüsselungsmethoden (z.B. DES) nicht mehr sicher vor Bruteforce-Angriffen waren.
Das Verfahren kann mit Hilfe einer Animation innerhalb von CrypTool 1 visualisiert und den SuS veranschaulicht werden. Dabei werden die einzelnen Runden des Verfahrens durchlaufen und erklärt. Menüpunkt: Einzelverfahren → Visualisierung von Algorithmen → AES → Rijndael-Animation.
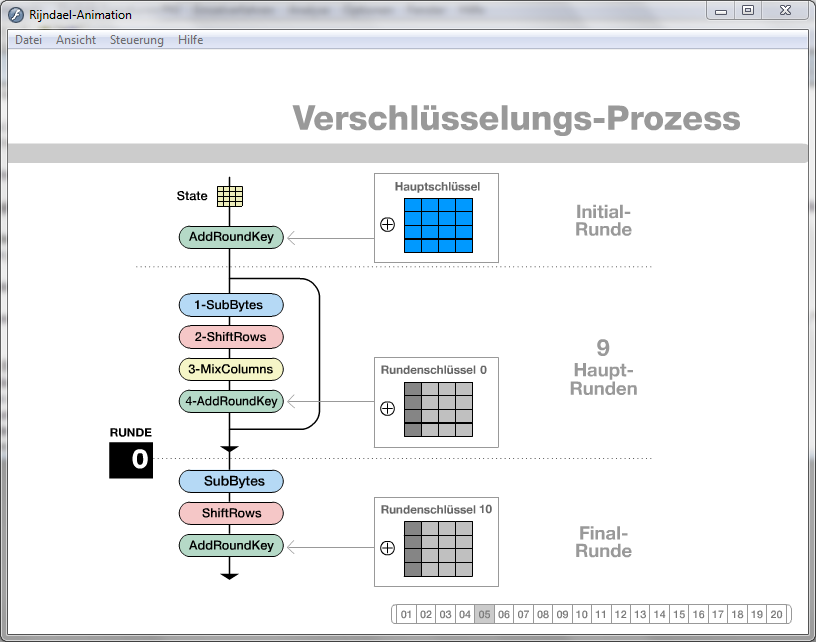
Quelle: Screenshot: CrypTool 1 (Version 1.4.30), www.cryptool.org
Die CrypTool-Visualisierung wird den SuS vorgeführt und dabei die einzelnen Schritte besprochen.
In Dia 03 sieht man eine Klartextblock (4x4). Beim AES-Verfahren wird der Klartext in mehrere 4x4 Blöcke geschrieben. Jede Zelle ist 1 Byte groß, beinhaltet also genau eine Hexadezimalzahl. Der Schlüssel ist ebenfalls ein 4x4 Block mit Hexadezimalzahlen.
In Dia 05 erkennt man den Prozess der Verschlüsselung, bei dem 11 Runden nacheinander ausgeführt werden (Initial-Runde, 9 Haupt-Runden, Final-Runde).
Dia 06 enthält die vier Verschlüsselungs-Transformationen, die nachfolgend vorgeführt werden.
In SubBytes (Dia 07) wird jedes Byte des 'Klartextes' durch ein anderes Byte ersetzt. Das ist eine monoalphabetische Substitution, genau wie z.B. beim Cäsar-Verfahren. Die S-Box entspricht dabei der Cäsar-Scheibe. Hinweis: der Klartext in dieser Runde ist nicht mehr 'klar', weil er in der Initial-Runde bereits verschlüsselt wurde.
In Shift-Rows (Dia 08) werden die Bytes zeilenweise rotiert. In jeder Zeile des Klartextblocks werden die Bytes nach links verschoben. Die links 'herausgefallenen' Bytes werden von rechts wieder hinzugefügt. In der zweiten Zeile wird um ein Byte, in der dritten Zeile um zwei Byte und in der vierten Zeile um drei Byte verschoben. Das ist leicht als Transposition erkennbar.
MixColums in Dia 09 ist für die Schüler zu komplex. (Anmerkung: Jede Spalte des Klartextblocks wird mit einer 4x4-Matrix multipliziert (modulo im Galois-Körper mit XOR). Das Ergebnis ist jeweils die veränderte neue Spalte.)
Bei AddRoundKey (Dia 10) wird jedes Byte des 'Klartextes' mit dem entsprechenden Byte des Rundenschlüssels mit XOR verknüpft. Allerdings ist XOR laut Bildungsplan erst in Klasse 9 vorgesehen. Daher sollte man Dia 09 und 10 nicht weiter thematisieren.
In Dia 11 sieht man, wie sich der Klartext von Runde zu Runde verändert, bis der Geheimtext entstanden ist.
In Dia 14 bis 20 wird die Generierung der Rundenschlüssel aus dem Hauptschlüssel gezeigt, worauf aber nicht weiter eingegangen werden soll. Es genügt, dass aus dem eigentlichen Schlüssel weitere 10 Schlüssel erzeugt werden, die in Runde 2-11 verwendet werden.
Die Entschlüsselung erfolgt dann analog in umgekehrter Reihenfolge.
Dadurch, dass verschiedene Verschlüsselungsverfahren mehrfach hintereinander ausgeführt werden, bietet das AES ein hohes Maß an Sicherheit, trotz des relativ kurzen Schlüssels von 128 Bit. Das Problem des Schlüsseltauschs ist bei AES, wie bei allen symmetrischen Verfahren, vorhanden, ist aber entschärft durch die Kürze des Schlüssels. Im Vergleich dazu ist OTP zwar sicher, aber nicht prakikabel.
Hinweis:
Da in der CrypTool1-Visualisierung Hexadezimalzahlen verwendet werden, ist es von Vorteil, wenn in IMP-Mathe bereits die Hexadezimalzahlen behandelt wurden (3.1.2.1 Mathematische Grundlagen der Kryptologie).
Zusatz:
Für weitergehende Informationen:
-
CrypTool 1
-
https://de.wikipedia.org/wiki/Advanced_Encryption_Standardhttps://de.wikipedia.org/wiki/Advanced_Encryption_Standard (Abgerufen am 4.4.18)
1 https://www.cryptool.org/de/ (Abgerufen am 8.5.18)
Unterrichtsverlauf: Herunterladen [odt][1 MB]
Unterrichtsverlauf: Herunterladen [pdf][1 MB]
Weiter zu Verschlüsselung eigener Daten
