Übungen ¹

Quelle: ZPG IMP

¹Leider gibt es keine einheitliche Schreibweise um kenntlich zu machen, dass man sich im Binärsystem befindet. Wir verwenden hier (und auf den folgenden Arbeitsblättern) die Schreibweise mit der tiefgestellten 2 unten rechts. Es gibt aber auch andere Schreibweisen, z.B. eine Klammer mit einer tiefgestellten 2 oder auch nur ein kleines b am Ende der Zahl. Es ist also alles dasselbe, nur anders aufgeschrieben: 1101₂ = (1101)₂ = 1101b.

Ohne Fleiß, kein Preis. Auch die besten Agenten benötigen ein paar Übungen, selbst wenn sie das System durchschaut haben. Deshalb lauten deine

Aufträge:

1. Notiere im jeweils anderen Stellenwertsystem:

1. a.) Verdopple mindestens vier der Zahlen aus 1. und notiere sie im Binärsystem.

   

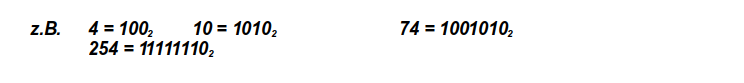
   b.) Vergleiche die „doppelten“ mit den „einfachen“ Zahlen. Was fällt dir auf?

   Die „doppelten“ Zahlen sind sehr ähnlich zu den „einfachen“ Zahlen: Es wird lediglich eine 0 hinten angefügt, sie sind also um eine Stelle länger.

   c.) Beschreibe kurz: Wie kann man gerade Zahlen im Binärsystem erkennen?

   Gerade Zahlen enden auf die Ziffer 0 im Binärsystem.

   *d.) Erfinde und erläutere ein Verfahren, um gerade Zahlen im Binärsystem zu halbieren.

   Man streicht die letzte Stelle. Diese muss „0“ gewesen sein, da es sich um gerade Zahlen handelte. Dadurch „verschiebt“ sich jede Ziffer um eine Stelle nach rechts. Benachbarte Stellen im Binärsystem unterscheiden sich um den Faktor 2. Wenn nach rechts verschoben wird, dann stehen die Ziffern jeweils an der Stelle, deren Wert um den Faktor 2 verkleinert , also halbiert wurde.

2. Ein Verfahren zur Umrechnung von dezimaler Schreibweise in die binäre Darstellung, das sich auch leicht programmieren lässt, wird hier am Beispiel der Zahl 41 aufgezeigt:

   

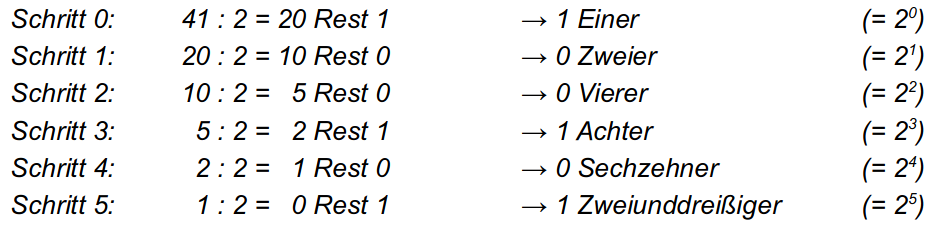
   Es folgt (von links nach rechts entspricht von unten nach oben): 41 = 101001₂

   a.) Rechne entsprechend die Zahlen 9, 19, 300 in das Binärsystem um.

   

   *b.) Erkläre, wie dieses Verfahren funktioniert. Überlege dazu, was die vollen Ergebnisse / die Reste der einzelnen Schritte jeweils mit den Stellennamen „Zweier, Vierer, ...“ zu tun haben.

   Klar wird das Verfahren, wenn man es mathematisch aufschreibt. Von Zeile zu Zeile wird dabei jeweils die darüber stehende fettgedruckte Zahl „halbiert“ und entsprechend notiert

   

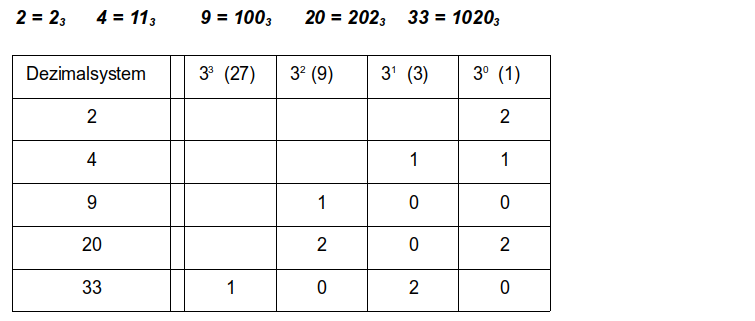
3. ** Das Binärsystem heißt auch Zweiersystem und das Dezimalsystem wird auch Zehnersystem genannt. Dies legt schon nahe, dass es noch weitere Stellenwertsysteme gibt. Erstelle entsprechende Regeln für das Dreiersystem und wandle die Zahlen 2, 4, 9, 20 und 33 in dieses System um.

   

 

 

Binärzahlen – Lösungen: Herunterladen [odt][1 MB]

Binärzahlen – Lösungen: Herunterladen [pdf][431 KB]

 

Weiter zu Knobelspaß