Hamiltonkreise – Übungen – Lösung

1.  

   

2. Europa per Bahn

   

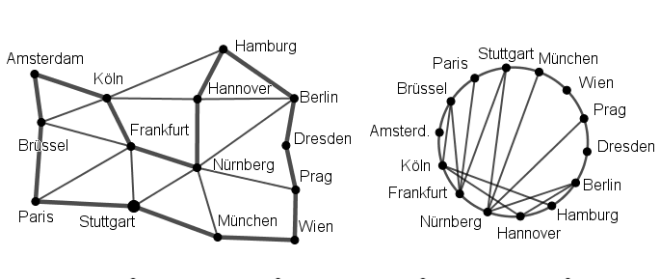
   Ja, der Hamilton-Kreis zeigt zwei mögliche Routen. Wenn man weitere suchen möchte, kann man mit dem gefundenen Hamiltonkreis, auch einen isomorphen, kreisförmigen Graphen zeichnen (siehe oben).

3. Regelmäßige Fünfecke

   

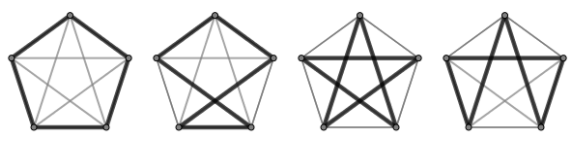
   Oben sind die vier möglichen geometrischen Formen zu sehen. Bei der ersten und dritten Figur könnte man in jedem der fünf Knoten starten und würde die gleiche rotationssymmetrische Figur erhalten. Bei der zweiten und vierten Figur verhält es sich anders. Hier erhält man jeweils fünf verschiedene Hamiltonkreise, wenn man an unterschiedlichen Knoten beginnt. Insgesamt gibt es also 1+5+1+5=12 Hamiltonkreise in einem vollständigen Graphen mit fünf Knoten.

4. LKW-Tour

   a) Der Routenvorschlag des Fahrers wäre 333 km lang, es gibt eine kürzere Route.

   

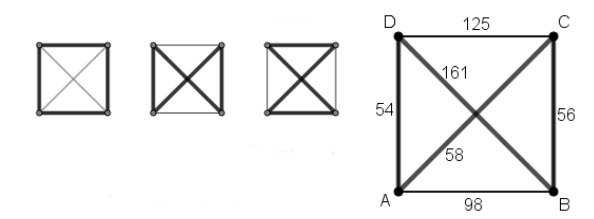
   b) Der bewertete Graph ist ein vollständiger Graph mit 4 Knoten und 6 Kanten. Er besitzt die 3 abgebildeten Hamiltonkreise, deren entsprechende Routen überprüft werden müssen:

   ABCDA (bzw. ADCBA): 333 km

   ABDCA (bzw. ACDBA): 442 km

   ADBCA (bzw. ACBDA): 329 km

   Der Fahrer sollte die Städte also in der Reihenfolge D,B,C anfahren.

   Hinweis: Die Anzahl der Hamiltonkreise in vollständigen Graphen mit n=3,4,5… Knoten wird schnell größer. Bei 5 Knoten sind es 12 (vgl. Aufgabe 3), bei 6 Knoten bereits 60 …, ohne geeignete Algorithmen käme man nicht weit!

5. Hamiltons Spielbrett

   

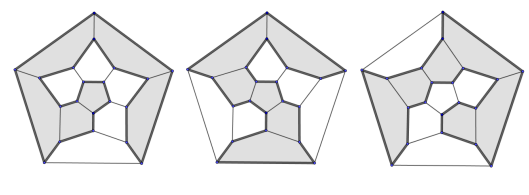
   Es gibt viele Möglichkeiten, hier sind drei abgebildet. Hamilton nannte sein Spiel übrigens „Traveller's Dodecahedron or A Voyage Round The World“. Es ging darum, eine vom Mitspieler begonnene Route durch 20 Metropolen der Welt zu einem Hamilton-Kreis zu ergänzen.

 

 

Hamiltonkreise – Übungen – Lösung: Herunterladen [odt][353 KB]

Hamiltonkreise – Übungen – Lösung: Herunterladen [pdf][272 KB]

 

Weiter zu Graphen als Tabellen