Der größ­te ge­mein­sa­me Tei­ler – ggT

Auf­trä­ge

1. Be­stim­me die fol­gen­den größ­ten ge­mein­sa­men Tei­ler:

   a.) ggT(12; 18)= 6

   b.) ggT(15; 45)= 15

   c.) ggT(64; 96)= 32

   d.) ggT(65; 91)= 13

2. Die Prim­fak­tor­zer­le­gun­gen meh­re­rer Zah­len las­sen sich ge­schickt ver­glei­chen, wenn man glei­che Prim­fak­to­ren un­ter­ein­an­der schreibt, z.B. für die Zah­len 300 und 630 so:

   

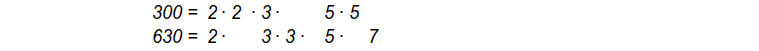
   a.) Führe dies für die Zah­len aus Auf­ga­be 1 durch. Schrei­be dazu für jede Teil­auf­ga­be die Prim­fak­tor­zer­le­gun­gen der bei­den Zah­len und des ggT in drei Zei­len un­ter­ein­an­der. Über­le­ge dir eine Regel, wie man aus den Prim­fak­tor­zer­le­gun­gen der bei­den Zah­len auf deren ggT kom­men kann, und schrei­be sie auf.

   Regel: Wenn man die Prim­fak­tor­zer­le­gun­gen der bei­den Zah­len spal­ten­wei­se zu­sor­tiert auf­schreibt, so er­hält man die Prim­fak­tor­zer­le­gung des ggT, indem man die Fak­to­ren ver­wen­det, die in jeder Zeile einer Spal­te vor­kom­men, alle an­de­ren nicht.

   

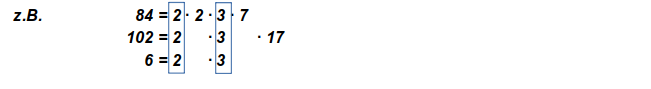
   b.) Über­prü­fe deine Regel an wei­te­ren Zah­len­paa­ren und deren ggT.

   In­di­vi­du­el­le Lsg.

   c.) Be­stim­me den ggT(9000; 41 580)

   

3. Der recht­ecki­ge Bal­kon des Agen­ten-Haupt­quar­tiers soll einen neuen Bo­den­be­lag aus mög­lichst gro­ßen, qua­dra­ti­schen Flie­sen be­kom­men. Dabei soll keine Flie­se zer­teilt wer­den. Wie groß soll­ten die Flie­sen sein, wenn der Bal­kon 6,75m breit und 3,60m tief ist?

   ggT(675; 360) = 45

   → Die Flie­ßen kön­nen eine ma­xi­ma­le Größe von 0,45m Sei­ten­län­ge haben

4. * „Der ggT kann beim Kür­zen von Brü­chen sehr hilf­reich sein.“

   Wie ist diese Aus­sa­ge ge­meint? Führe zu­nächst ei­ni­ge Ver­su­che an kürz­ba­ren Brü­chen durch. Über­le­ge dabei: Wie kann der ggT von Zäh­ler und Nen­ner ge­schickt ein­ge­setzt wer­den? Wie kann/ würde man ohne die Kennt­nis die­ses ggT vor­ge­hen? For­mu­lie­re dann eine Vor­ge­hens­wei­se zum Kür­zen von Brü­chen, in der der ggT ein­ge­setzt wird. Ver­glei­che dann die bei­den Vor­ge­hens­wei­sen (Kür­zen mit / ohne Er­mitt­lung des ggT).

   Brü­che kann man Kür­zen, wenn Zäh­ler und Nen­ner einen ge­mein­sa­men Tei­ler haben. Wenn sie meh­re­re Tei­ler haben, dann kann man den „erst­bes­ten“ Tei­ler neh­men, der auf­fällt. Bei ge­ra­den Zah­len ist dies häu­fig die Zahl 2. Das Pro­blem dabei ist, dass der so ent­ste­hen­de Bruch zwar ge­kürzt ist, sich aber nicht sel­ten noch wei­ter kür­zen lässt. Wenn man da­ge­gen mit dem größ­ten ge­mein­sa­men Tei­ler kürzt, dann ent­steht ein voll­stän­dig ge­kürz­ter Bruch.

   

kgV und ggT – Lö­sun­gen: Her­un­ter­la­den [odt][2 MB]

Wei­ter zu Wei­te­re Übun­gen zu kgV und ggT