Das Sender-Empfänger-Spiel

Beim Sender-Empfänger-Spiel¹ simulieren die Schülerinnen und Schüler das Übertragen eines binär codierten Textes, wobei sich auf dem Übertragungsweg, der sogenannten Leitung, Fehler einschleichen sollen. Anhand zweier verschiedener Codetabellen wird die Güte eines Codes hinsichtlich der Fehlerkorrektur untersucht und beurteilt (zugehöriges Arbeitsblatt: 03_duc_ab_sender_empfaenger_spiel.odt). Die Untersuchung der Codes führt zur Hamming-Distanz, die auf Seite 4 des Arbeitsblattes behandelt wird.

Hinweis: Die Hamming-Distanz ist nicht Bestandteil des Bildungsplans und kann problemlos gestrichen werden. Sie wird hier als mögliches Zusatzmaterial aufgeführt.

Abschließend zur Unterrichtseinheit „Daten und Codieren“ können die Schülerinnen und Schüler die Vor- und Nachteile der Fehlerkorrektur auf unterschiedliche Situationen übertragen.

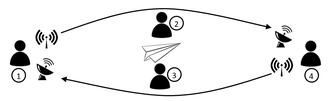
Für das Sender-Empfänger-Spiel wird die Klasse in Gruppen aufgeteilt. Dabei besteht eine Gruppe aus drei Positionen: Sender (), Leitung (), Empfänger (). Die Position Leitung wird doppelt besetzt.

Es wird empfohlen, das Spiel gut vorzubereiten und es den Schülerinnen und Schülern ausführlich zu erklären, damit ein reibungsloser Ablauf auch bei größeren Schülergruppen gewährleistet ist.

1. Ablauf des Spiels

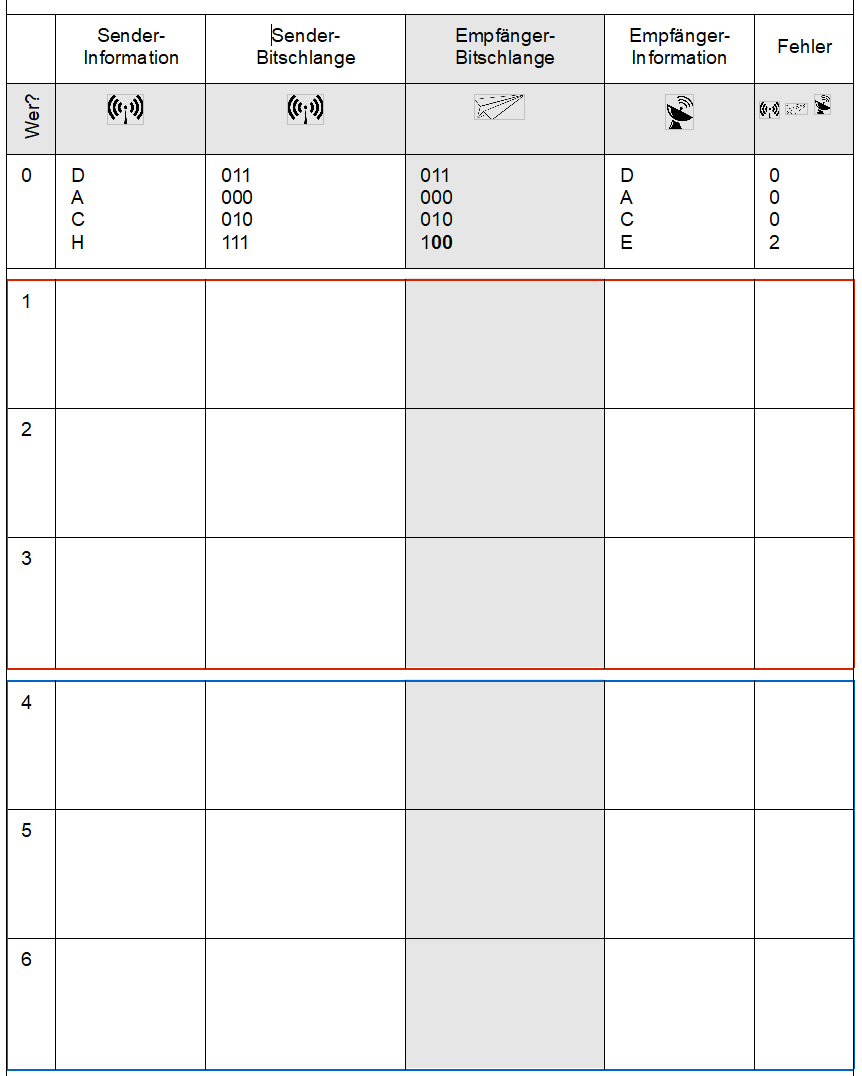
Alle Schülerinnen und Schüler bekommen die nebenstehende Tabelle (vgl. Arbeitsblatt, Seite 2), in die sie ihre Eintragungen machen sollen. In Zeile 0 ist bereits ein Beispiel zur Erläuterung eingetragen.

Die Positionen 1-4 innerhalb einer Gruppe sind wie folgt besetzt:

Des Weiteren werden zwei Codetabellen „Alpha“ und „Beta“ benötigt, die auch als Vorlage unter 03_duc_kopiervorlage_Codetabellen.odt zu finden sind:

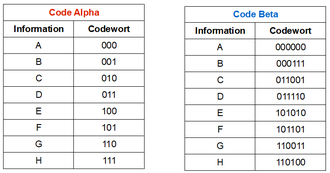
Jeweils die Positionen 1 und 4 (Sender und Empfänger ) bekommen zunächst den Code Alpha und im zweiten Teil des Spiels den Code Beta.

Die Positionen 2 und 3 (Leitung ) benötigen je einen Würfel, mit dem zufällige Fehler simuliert werden sollen. Wahlweise kann anstatt eines Würfels auch die Random-Funktion eines WTRs verwendet werden.

Der Sender beginnt in der Zeile 1 und notiert in der ersten Spalte „Sender-Information“ ein Wort (sinnvoll oder nicht) mit vier Buchstaben. In der zweiten Spalte „Sender-Bitschlange“ codiert er das Wort buchstabenweise entsprechend Codetabelle Alpha.

Der Sender übergibt das Blatt an die Leitung . Nun wird für jedes Bit der Sender-Bitschlange gewürfelt:

• Bei einer 6 wird statt einer 0 eine 1 bzw. statt einer 1 eine 0 eingetragen.
• Bei einer 1-5 wird das Bit unverändert übernommen.

Diese ggf. geänderte Bitfolge wird von der Leitung in die Spalte „Empfänger-Bitschlange“ eingetragen. Anschließend wird das Arbeitsblatt links der grauen Spalte gefaltet, sodass die drei rechten Spalten nach oben liegen. Die Leitung übergibt das gefaltete Arbeitsblatt an den Empfänger weiter.

Der Empfänger hat nun die Aufgabe, die Bitschlange zu decodieren und das empfangene Wort in die Spalte „Empfänger-Information“ der Tabelle einzutragen. Dabei soll in folgenden Schritten vorgegangen werden:

1. Ist das Decodieren eindeutig möglich, dann ist alles prima.
2. Ist das Decodieren nicht eindeutig möglich, dann soll „bestmöglich“ decodiert werden. Das bedeutet, dass derjenige Buchstabe gewählt werden soll, der sich an den wenigsten Stellen (Bits) vom Code unterscheidet. Gibt es hierbei zwei Möglichkeiten, soll zufällig entschieden werden.

Anschließend wird innerhalb der Gruppe das Geheimnis gelüftet und gezählt, wie viele Fehler bei der Übertragung gemacht wurden. Dies wird in die letzte Spalte eingetragen.

Um am Ende des gesamten Spiels für das Zusammentragen und Auswerten im Hinblick auf die Güte eines Codes genügend Ergebnisse zu sammeln, kann diese Runde mit der Codetabelle Alpha noch einmal wiederholt werden. Dazu tauschen die Positionen 1 und 2 sowie 3 und 4 ihre Rollen und tragen ein neues Wort in Zeile 2 ein.

Zeile 3 dient lediglich als Puffer für besonders schnelle Gruppen.

Wenn auch auch diese Runde vorbei ist, wird obiges analog mit der zweiten Codetabelle Beta durchgeführt.

2. Güte eines Codes

Nachdem alle Fehlerzahlen in der letzten Spalte eingetragen wurden, werden nun in der gesamten Klasse die Ergebnisse gesammelt und in die Tabelle auf Seite 5 des Arbeitsblattes eingetragen. Dabei wird deutlich, dass bei gleicher Anzahl versendeter Wörter sich die Positionen „korrekt erkannte Buchstaben“ und „versendete Signale (Bits)“ bei den beiden Codes Alpha und Beta unterscheiden.

Das gesammelte Ergebnis dient nun als Gesprächsgrundlage über einen Austausch über die Güte eines Codes. Die Schülerinnen und Schüler sollen erläutern, warum es zu dieser unterschiedlichen Zahl von Fehlern kommt.

Nachdem die Schülerinnen und Schüler zu dem Schluss gekommen sind, dass Code Beta wohl der „bessere“ Code sein muss, kann nun die daran folgende Aufgabe des Arbeitsblattes betrachtet werden, so dass die Schülerinnen und Schüler auch die Nachteile des Codes Beta erkennen sollen.

Die Entscheidung, wann eine hohe Fehlerkorrektur von großer Bedeutung ist und wann man auch auf Fehlerkorrektur verzichten kann, hängt immer von der Situation ab. Ein paar exemplarische Situationen sind in der letzten Aufgabe des Arbeitsblattes aufgeführt, zu denen die Schülerinnen und Schüler ihre Einschätzung abgeben können.

3. Die Hamming-Distanz

Als Ergänzung kann die Hamming-Distanz eingeführt werden. Wie bereits erwähnt, ist diese nicht Bestandteil des Bildungsplans. Ein Tutorial zur Bestimmung der Hamming-Distanz (auch Hamming-Abstand genannt) findet man beispielsweise unter dem Link https://www.youtube.com/watch?v=61kcq2RM8bo (letzter Aufruf: 30.04.2018). Codes mit einer höheren Hamming-Distanz sind robuster gegenüber Fehlern.

---

¹ In Anlehnung an Jens Gallenbacher, Abenteuer Informatik.

 

Unterrichtsverlauf: Herunterladen [odt][408 KB]

Unterrichtsverlauf: Herunterladen [pdf][1 MB]

 

Weiter zu Kopiervorlagen