Das kleins­te ge­mein­sa­me Viel­fa­che – kgV

Auf­trä­ge:

1. Be­stim­me die fol­gen­den kleins­ten ge­mein­sa­men Viel­fa­chen:

   a.) kgV(6; 7) = 42

   b.) kgV(12; 18) = 36

   c.) kgV(14; 18) = 126

   d.) kgV(84; 102) = 1428

2. Die Prim­fak­tor­zer­le­gun­gen meh­re­rer Zah­len las­sen sich ge­schickt ver­glei­chen, wenn man glei­che Prim­fak­to­ren un­ter­ein­an­der schreibt, z.B. für die Zah­len 300 und 630 so:

   

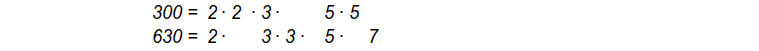
   a.) Führe dies für die Zah­len aus Auf­ga­be 1 durch. Schrei­be dazu für jede Teil­auf­ga­be die Prim­fak­tor­zer­le­gun­gen der bei­den Zah­len und des kgV in drei Zei­len un­ter­ein­an­der. Über­le­ge dir eine Regel, wie man aus den Prim­fak­tor­zer­le­gun­gen der bei­den Zah­len auf deren kgV kom­men kann, und schrei­be sie auf.

   Regel: Wenn man die Prim­fak­tor­zer­le­gun­gen der bei­den Zah­len spal­ten­wei­se zu­sor­tiert auf­schreibt, so er­hält man die Prim­fak­tor­zer­le­gung des kgV, indem man den Fak­tor aus jeder Spal­te ein­mal ver­wen­det – egal, ob er in bei­den Zah­len oder nur in einer der bei­den Zah­len vor­kommt.

   

   b.) Über­prü­fe deine Regel an wei­te­ren Zah­len­paa­ren und deren kgV.

   In­di­vi­du­el­le Lsg.

   c.) Be­stim­me das kgV(9000; 41580)

   

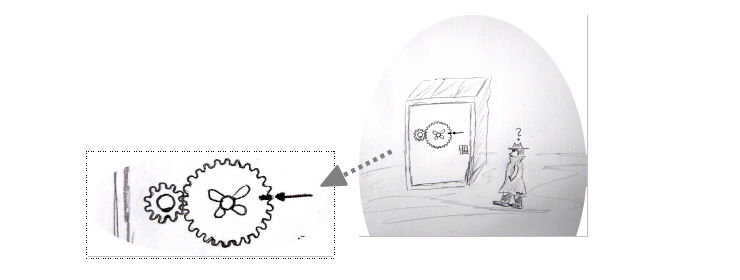
3. Agent Mü muss mal wie­der einen Tre­sor kna­cken. Da­zu­muss er eine Zahl auf einem Zif­fern­feld ein­ge­ben. Die­Ein­ga­be­zahl lässt ein klei­nes Zah­len­rad genau so oft um sich­selbst dre­hen. Der Tre­sor geht auf, wenn sich da­durch das­gro­ße Zah­len­rad wie­der an der glei­chen Po­si­ti­on wie vor der­Ein­ga­be be­fin­det. Was muss er ein­ge­ben?

   

   Quel­le: ZPG IMP

   Nach­zäh­len er­gibt beim klei­nen Zahn­rad 11 Zähne und beim gro­ßen Zahn­rad 26 Zähne. Da kgV(11; 26) = 286, muss man das klei­ne Zahn­rad 26 Mal dre­hen, damit sich das große Rad wie­der an der glei­chen Po­si­ti­on be­fin­det (die­ses dreh­te sich dann 11 Mal).

1. * „Das kgV kann bei der Ad­di­ti­on und Sub­trak­ti­on von Brü­chen sehr hilf­reich sein.“

   Wie ist diese Aus­sa­ge ge­meint? Führe zu­nächst ei­ni­ge Bei­spiel­ad­di­tio­nen von Brü­chen durch. Über­le­ge dabei: Wie kann das kgV wel­cher Zah­len ge­schickt ein­ge­setzt wer­den? Wie kann / würde man ohne die Kennt­nis die­ses kgV vor­ge­hen? For­mu­lie­re dann eine Vor­ge­hens­wei­se zur Ad­di­ti­on und Sub­trak­ti­on von Brü­chen, in der das kgV (ge­schickt) ein­ge­setzt wird.

   Bei der Ad­di­ti­on / Sub­trak­ti­on zwei­er Brü­che be­nö­tigt man einen Haupt­nen­ner / ge­mein­sa­men Nen­ner. Die­ser kann er­zeugt wer­den, indem man die bei­den Nen­ner mul­ti­pli­ziert. Dabei ent­ste­hen je­doch unter Um­stän­den sehr hohe Zah­len als Zäh­ler und Nen­ner. Der kleins­te ge­mein­sa­me Nen­ner ist das kleins­te ge­mein­sa­me Viel­fa­che der bei­den Nen­ner. So blei­ben die zu ad­die­ren­den Zäh­ler-Zah­len ins­ge­samt kleinst­mög­lich.

   

kgV und ggT – Lö­sun­gen: Her­un­ter­la­den [odt][2 MB]

kgV und ggT – Lö­sun­gen: Her­un­ter­la­den [pdf][463 KB]

Wei­ter zu ggT