Re­chen­ver­fah­ren

Auf­trä­ge in Part­ner­ar­beit:

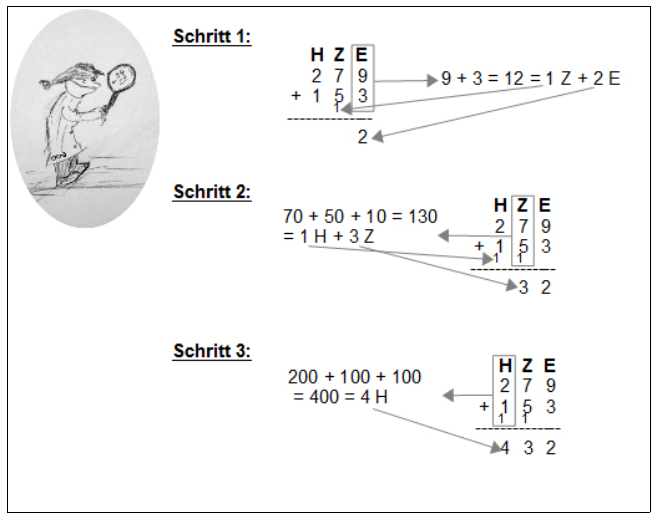
Quel­le: ZPG IMP

1. In der Ab­bil­dung oben ist das schrift­li­che Re­chen­ver­fah­ren zur Ad­di­ti­on mit­hil­fe des Über­tra­ges an einem aus­führ­li­chen Bei­spiel dar­ge­stellt.

   a.) Über­tragt das Ad­di­ti­ons­ver­fah­ren auf das Bi­närs­ys­tem, be­rech­net und no­tiert dazu in ver­gleich­ba­rer Art und Weise die Ad­di­ti­on 1012 + 112 .

   P.S.: Ihr dürft gerne Far­ben ein­set­zen, um eure Dar­stel­lung über­sicht­li­cher zu ge­stal­ten.

   P.P.S.: Hil­fe­kärt­chen lie­gen be­reit, falls ihr nicht wei­ter­kommt.

   b.) Be­rech­net mit­hil­fe die­ses Ad­di­ti­ons­ver­fah­rens die fol­gen­den Sum­men:

   1001₂ + 1100₂

   1111₂ + 1010₂

   1111₂ + 1111₂

2. Ihr sollt nun ein wei­te­res, euch im de­zi­ma­len Stel­len­wert­sys­tem be­kann­tes schrift­li­ches Re­chen­ver­fah­ren auf das Bi­närs­ys­tem über­tra­gen. Wählt dazu min­des­tens eine der fol­gen­den Auf­ga­ben aus:

   • Sub­trak­ti­on:

     Führt die schrift­li­che Sub­trak­ti­on 31 – 13 schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und sub­tra­hiert 11011₂ – 1101₂

   • Di­vi­son ohne Rest

     Führt die schrift­li­che Di­vi­si­on 465 : 15 schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und di­vi­diert 1100₂ : 10₂

   • Mul­ti­pli­ka­ti­on

     Führt die schrift­li­che Mul­ti­pli­ka­ti­on 123 · 72 schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und mul­ti­pli­ziert 11011₂ · 1011₂

   • (**) Zu­satz­auf­ga­be: Di­vi­si­on mit Rest

     Führt die schrift­li­che Di­vi­si­on für 123 : 7 mit Rest schritt­wei­se durch und macht euch die Be­deu­tung eurer Schrit­te im Stel­len­wert­sys­tem klar. Über­tragt diese Be­deu­tung dann auf das Bi­närs­ys­tem und di­vi­diert 1011₂ : 11₂

Bi­n­är­zah­len-Re­chen­ver­fah­ren, Auf­ga­be 1., Hil­fe­kärt­chen 1:

Schrei­be die Zah­len rechts­bün­dig un­ter­ein­an­der, so wie du das vom schrift­li­chen Rech­nen im De­zi­mal­sys­tem her ge­wöhnt bist.

Ad­die­re dann – auch wie ge­wohnt – von rechts nach links spal­ten­wei­se die Einer. Du er­hältst als Summe zwei Einer. Was be­deu­tet das im Bi­närs­ys­tem?

Bi­n­är­zah­len-Re­chen­ver­fah­ren, Auf­ga­be 1., Hil­fe­kärt­chen 2:

Du hast im vo­ri­gen Schritt die Ei­ner­stel­len ad­diert und 2 Einer er­hal­ten. Es gibt je­doch im Bi­närs­ys­tem keine Zif­fer „2“. Dafür ist die zwei­te Stel­le (von rechts) die Stel­le für die 21-er, also die 2-er. Somit wer­den die zwei Einer als 1 Zwei­er über­tra­gen, es blei­ben 0 Einer übrig:

Bi­n­är­zah­len-Re­chen­ver­fah­ren, Auf­ga­be 1., Hil­fe­kärt­chen 3:

Jetzt geht es ei­gent­lich wei­ter „wie immer“: In der zwei­ten Spal­te, das ist die Zwei­er­spal­te ad­dierst du nun die bei­den 0-Ein­trä­ge und die über­tra­ge­ne 1 und er­hältst

Fehlt noch die letz­te Spal­te, das ist die Vie­rer-Spal­te (=2²).

Bi­n­är­zah­len – Übun­gen zu den Re­chen­ver­fah­ren

Quel­le: ZPG IMP

Min­des­tens zwei der fol­gen­den Auf­ga­ben a.) bis d.) soll­tet ihr nun ohne wei­te­re Hilfe lösen kön­nen. Führt dies zu­nächst ein­zeln durch und ver­gleicht dann eure Er­geb­nis­se.

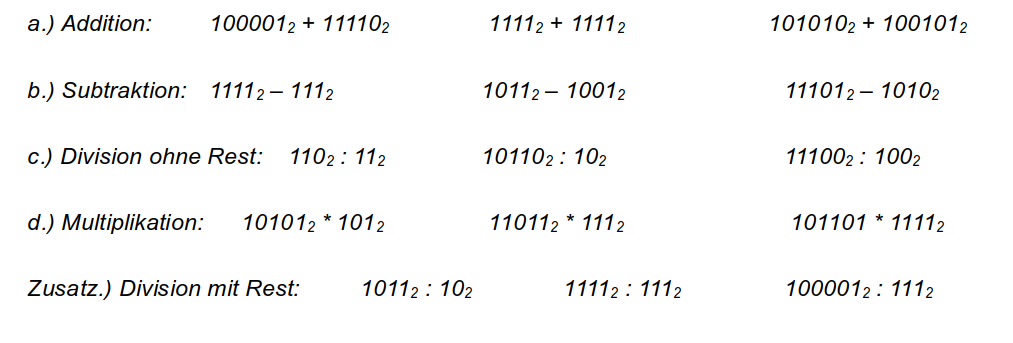
* Tauscht euch mit einer Zwei­er­grup­pe aus, die ein an­de­res schrift­li­ches Re­chen­ver­fah­ren er­ar­bei­tet hat. Er­klärt euch eure un­ter­schied­li­chen Ver­fah­ren ge­gen­sei­tig und löst dann die zu­ge­hö­ri­gen Teil­auf­ga­ben wie­der zu­erst in Ein­zel­ar­beit.

Re­chen­ver­fah­ren: Her­un­ter­la­den [odt][310 KB]

Re­chen­ver­fah­ren: Her­un­ter­la­den [pdf][160 KB]

Wei­ter zu He­xa­de­zi­mal­zah­len