Bestimmtheitsmaß
In den folgenden drei Bildern symbolisieren die roten, ausgefüllten Flächen
die Summe der quadratischen Abweichungen von der Ausgleichsgeraden (Regressionsgeraden,
Trendlinie). Für diese Summe gilt:
|
|
Die grünen, schraffierten Flächen stellen zum Vergleich die Summe der quadratischen Abweichungen vom Mittelwert dar, d. h. es ist
|
|
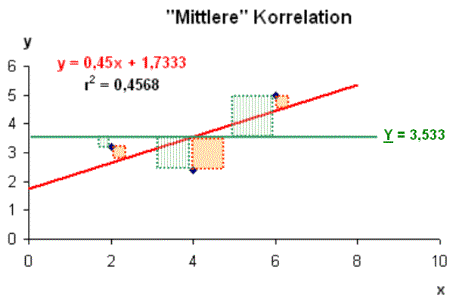
Bild 1: Mäßige Korrelation der Messwerte mit der
Ausgleichsgeraden g: y = m·x + b
|
|
Diese beiden Flächen A Regr und A Mittel werden jeweils verglichen, um ein Maß für die Bestimmtheit r 2 bzw. Korrelation r (Übereinstimmung) zu gewinnen. Die Bestimmtheit r 2 ist definiert durch |
|
r
2
= 1 – A
Regr
/ A
Mittel
|
Um dies zu verstehen, betrachten wir die Extremfälle von Bild 2 und Bild 3.
In
Bild 2
(vollständige Korrelation) liegen die Messwerte exakt auf
der (roten) Ausgleichsgeraden. Deshalb ist A
Regr
= 0 und
somit auch
A
Regr
/ A
Mittel
= 0. Mit anderen Worten:
Für die Bestimmtheit folgt
r
2
= 1 – A
Regr
/ A
Mittel
= 1 – 0 = 1
,
also eine 100%ige Korrelation.
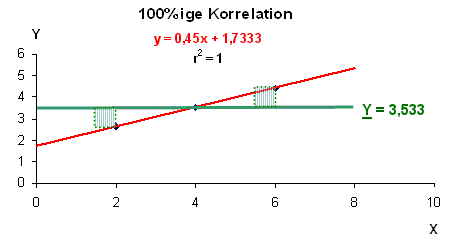
Bild 2: Absolute Übereinstimmung der Messwerte mit der Ausgleichsgeraden
In
Bild 3
(keine erkennbare Korrelation) sind die beiden Flächen A
Regr
und A
Mittel
gleich groß, d. h. es gilt A
Regr
/ A
Mittel
= 1 und deshalb ist
r 2 = 1 – A Regr / A Mittel = 1 – 1 = 0
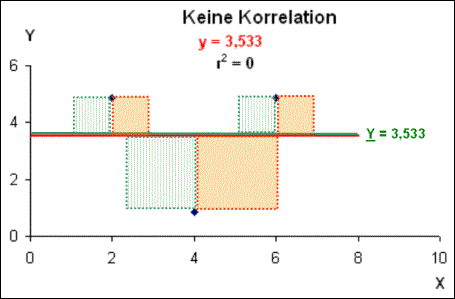
Bild 3: Messwerte ohne Korrelation
Zurück zu
Bild 1:
Hier liefert ein Flächenvergleich
A
Regr
/ A
Mittel
= 0,5432, weshalb
für r
2
folgt:
r 2 = 1 – A Regr / A Mittel = 1 – 0,5432 = 0,4568
Der Wert des Korrelationskoeffizienten r beträgt somit rund 68%.
