Regression

Im einfachsten Fall ist der Zusammenhang zweier Datenreihen (Merkmale) annähernd linear, d. h. er kann gut durch eine „Ausgleichsgerade“ beschrieben werden. Eine solche Anpassungsgerade heißt auch Regressionsgerade oder Trendlinie. Diese legen Schülerinnen und Schüler oft nach „Gefühl“ durch ihre Messpunkte, was zu einer nicht eindeutigen Darstellung führt.

Die Methode der kleinsten Abweichungsquadrate liefert jedoch eine eindeutige Gleichung für die Regressionsgerade. Es gilt dann:

Eine Regressionsgerade mit der Gleichung

hat die Steigung

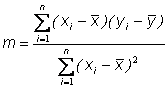
und den

y- Achsenabschnitt

,

wobei  die üblichen arithmetischen Mittelwerte und der Punkt
 den Schwerpunkt darstellen.

Fast alle Taschenrechner und Tabellenkalkulationsprogramme erstellen Ausgleichsgeraden auf Knopfdruck!

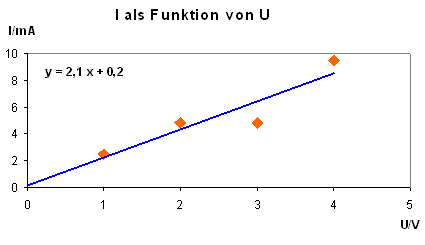
Beispiel mit eingeblendeter Ausgleichsgerade: y = 2,1·x + 0,2

Neben der linearen Regression werden von Rechnern auch Trendlinien höherer Ordnung , wie polynomische, exponentielle und logarithmische angeboten.

Die Ausgleichsgerade, kurz erklärt               Diese Grafik vergrößern