Korrelation
Daten können dieselbe Ausgleichsgerade haben, aber doch sehr unterschiedlich
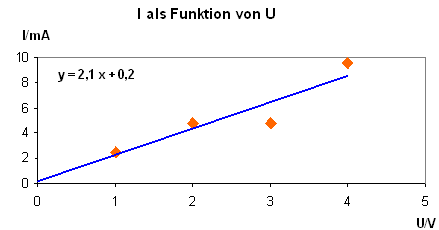
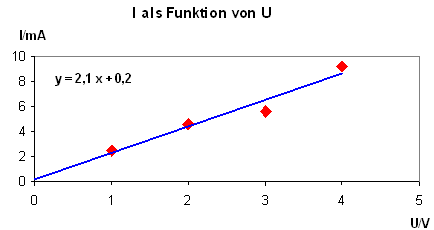
um diese verteilt sein. Dies zeigt oft schon der Augenschein (siehe Schaubild
1 im Vergleich zu Schaubild 2):
|
Schaubild 1: r
2
= 0,85, also
r = 0,92
|
|
Schaubild 2: r
2
= 0,90, also
r = 0,95
|
Um diesen Unterschied mathematisch eindeutig zu beschreiben, wurde ein so genanntes
Bestimmtheitsmaß r
2
bzw. der
Korrelationskoeffizient
r
eingeführt.
- Der Korrelationskoeffizient r nimmt nur Werte zwischen + 1 und – 1 an. (Er hat das Vorzeichen der Geradensteigung m.)
- Liegt der Wert nahe bei + 1 oder – 1, so spricht man von einem guten bis sehr guten Zusammenhang der Datenreihen. Beim Schaubild 2 streuen die Punkte demnach weniger.
- Liegt der Wert nahe bei 0, so spricht man von einem schlechten Zusammenhang der Datenreihen.
Die hierzu entwickelten Formeln sprengen den Rahmen einer manuellen Berechnung. Sie sind in Taschenrechnern und Tabellenkalkulationsprogrammen standardmäßig hinterlegt.
- Den Grundgedanken zur Festlegung des Bestimmtheitsmaßes r 2 können Sie hier einsehen.
Die von Rechnern ebenfalls angebotenen Trendlinien höherer Ordnung werden durch eine geeignete Transformation auf lineare Regressionen zurückgeführt.
Beispiel:
Aus y = a·x
2
folgt der lineare Zusammenhang ln(y) = 2·ln(x)
+ ln(a).
